作出下列函数的图象(1)y=|x-2|(x+1);(2)y=10|lgx|.
分析:(1)本题是一个含有绝对值的函数,故在作图时要去掉绝对值号,变为分段函数,研究其单调性与特殊点,做出函数的示意图.
(2) y=10|lgx| 可以以变为一分段函数,然后研究其性质,作出其图象.
解答: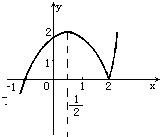
解:(1)当x≥2时,即x-2≥0时,y=x
2-x-2=
(x-)2-当x<2时,即x-2<0时,y=-x
2+x+2=-
(x-)2+∴y=|x-2|(x+1)=
这是分段函数,每段函数图象可根据二次函数图象作出(见图)
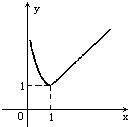
(2)当x≥1时,lgx≥0,y=10
|lgx|=10
lgx=x;
当0<x<1时,lgx<0,y=10-
|lgx|=10
lg=
;
故有y=10
|lgx|=
这是分段函数,每段函数可根据正比例函数或反比例函数作出.(见图)
点评:本题考点是对数函数的图象与性质,考查含有绝对值的函数的图象的画法,一般此类函数都是先转化为分段函数,再根据每一段上的表达式作出相应函数的图象来.

 解:(1)当x≥2时,即x-2≥0时,y=x2-x-2=(x-
解:(1)当x≥2时,即x-2≥0时,y=x2-x-2=(x- (2)当x≥1时,lgx≥0,y=10|lgx|=10lgx=x;
(2)当x≥1时,lgx≥0,y=10|lgx|=10lgx=x;
