
【题目】设a>0, ![]() 是R上的偶函数.
是R上的偶函数.
(1)求a的值;
(2)证明f(x)在(0,+∞)上为增函数.
【答案】
(1)解:依题意,对一切x∈R,有f(﹣x)=f(x),即 ![]()
∴ ![]() =0对一切x∈R成立,则
=0对一切x∈R成立,则 ![]() ,∴a=±1,∵a>0,∴a=1
,∴a=±1,∵a>0,∴a=1
(2)证明:设0<x1<x2,则 ![]()
= ![]() ,
,
由x1>0,x2>0,x2﹣x1>0,
得 ![]() ,
,
得 ![]() ,
,
∴f(x1)﹣f(x2)<0,
即f(x1)<f(x2),∴f(x)在(0,+∞)上为增函数
【解析】(1)根据偶函数的定义f(﹣x)=f(x)即可得到答案.(2)用定义法设0<x1<x2 , 代入作差可得.
【考点精析】掌握函数单调性的判断方法和函数的偶函数是解答本题的根本,需要知道单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较;一般地,对于函数f(x)的定义域内的任意一个x,都有f(-x)=f(x),那么f(x)就叫做偶函数.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy 中,椭圆G的中心为坐标原点,左焦点为F1(﹣1,0),离心率e=![]() .
.
(1)求椭圆G 的标准方程;
(2)已知直线l1:y=kx+m1与椭圆G交于 A,B两点,直线l2:y=kx+m2(m1≠m2)与椭圆G交于C,D两点,且|AB|=|CD|,如图所示.
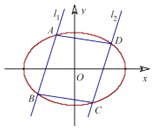
①证明:m1+m2=0;
②求四边形ABCD 的面积S 的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=log2(x+1),g(x)=log2(3x+1).
(1)求出使g(x)≥f(x)成立的x的取值范围;
(2)当x∈[0,+∞)时,求函数y=g(x)﹣f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在R上不恒为0的函数,且对于任意的实数a,b满足f(2)=2,f(ab)=af(b)+bf(a),an= ![]() (n∈N*),bn=
(n∈N*),bn= ![]() (n∈N*),给出下列命题:
(n∈N*),给出下列命题:
①f(0)=f(1);
②f(x)为奇函数;
③数列{an}为等差数列;
④数列{bn}为等比数列.
其中正确的命题是 . (写出所有正确命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】提高过江大桥的车辆通行能力可改善整个城市的交通状况.在一般情况下,大桥上的车流速度v(单位:千米/小时)是车流密度x(单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时.研究表明:当![]() 时,车流速度
时,车流速度![]() 是车流密度
是车流密度![]() 的一次函数.
的一次函数.
(1)当![]() 时,求函数
时,求函数![]() 的表达式;
的表达式;
(2)当车流密度![]() 为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)
为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)![]() 可以达到最大,并求出最大值.(精确到1辆/小时)
可以达到最大,并求出最大值.(精确到1辆/小时)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在等差数列{an}中,a2+a7=﹣23,a3+a8=﹣29.
(1)求数列{an}的通项公式;
(2)设数列{an+bn}是首项为1,公比为c的等比数列,求{bn}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法中,正确的是
·(1)任取x>0,均有3x>2x;
·(2)当a>0,且a≠1时,有a3>a2;
·(3)y=( ![]() )﹣x是减函数;
)﹣x是减函数;
·(4)函数f(x)在x>0时是增函数,x<0也是增函数,所以f(x)是增函数;
·(5)若函数f(x)=ax2+bx+2与x轴没有交点,则b2﹣8a<0且a>0;
·(6)y=x2﹣2|x|﹣3的递增区间为[1,+∞).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若二次函数f(x)=ax2+bx+c(a,b,c∈R)满足f(x+1)﹣f(x)=4x+1,且f(0)=3.
(1)求f(x)的解析式;
(2)若在区间[﹣1,1]上,不等式f(x)>6x+m恒成立,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com