
【题目】已知抛物线C:x2=2py(p>0)的焦点到直线l:2x﹣y﹣1=0的距离为![]() .
.
(1)求抛物线的方程;
(2)过点P(0,t)(t>0)的直线l与抛物线C交于A,B两点,交x轴于点Q,若抛物线C上总存在点M(异于原点O),使得∠PMQ=∠AMB=90°,求实数t的取值范围.
【答案】(1)x2=y;(2)t≥1.
【解析】
(1)直接利用点到直线的距离公式计算得到答案.
(2)过点P(0,t)(t>0)的直线l的方程设为y=kx+t,联立方程,利用韦达定理得到x1+x2=k,x1x2=﹣t,且y1=x12,y2=x22,根据∠PMQ=∠AMB=90°,可得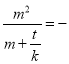
![]() 1,化简得到答案.
1,化简得到答案.
(1)抛物线C:x2=2py(p>0)的焦点(0,![]() )到直线l:2x﹣y﹣1=0的距离为
)到直线l:2x﹣y﹣1=0的距离为![]() ,
,
可得![]() ,解得p
,解得p![]() ,即抛物线的方程为x2=y;
,即抛物线的方程为x2=y;
(2)过点P(0,t)(t>0)的直线l的方程设为y=kx+t,联立x2=y,可得x2﹣kx﹣t=0,
设A(x1,y1),B(x2,y2),可得k2+4t>0,x1+x2=k,x1x2=﹣t,且y1=x12,y2=x22,
设M(m,m2),Q(![]() ,0),
,0),
由∠PMQ=∠AMB=90°,可得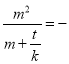
![]() 1,化为
1,化为![]() m3﹣mt+m,①
m3﹣mt+m,①
![]()
![]() 1,即(m+x1)(m+x2)=﹣1,化为m2+km﹣t+1=0,②
1,即(m+x1)(m+x2)=﹣1,化为m2+km﹣t+1=0,②
由①②可得t=k2m2,
由k2﹣4(1﹣t)≥0可得4(1﹣t)≤k2![]() ,
,
由于m≠0,m2>0,可得![]() 0解得t≥1.
0解得t≥1.


科目:高中数学 来源: 题型:
【题目】已知![]() 的定义域为
的定义域为![]() ,
,![]() ,使得不等式
,使得不等式![]() 成立,关于
成立,关于![]() 的不等式
的不等式![]() 的解集记为
的解集记为![]() .
.
(1)若![]() 为真,求实数
为真,求实数![]() 的取值集合
的取值集合![]() ;
;
(2)在(1)的条件下,若![]() 是
是![]() 的充分不必要条件,求实数
的充分不必要条件,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种产品的质量以其质量指标值衡量,并依据质量指标值划分等级如表:
质量指标值m | 25≤m<35 | 15≤m<25或35≤m<45 | 0<m<15或45≤m≤65 |
等级 | 一等品 | 二等品 | 三等品 |
某企业从生产的这种产品中抽取100件产品作为样本,检测其质量指标值,得到如图所示的频率分布直方图.(同一组数据用该区间的中点值作代表):
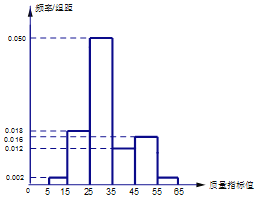
(1)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“一、二等品至少要占全部产品82%”的规定?
(2)该企业为提高产品质量,开展了“质量提升月”活动,活动后再抽样检测,产品质量指标值X近似满足X~N(31,122),则“质量提升月”活动后的质量指标值的均值比活动前大约提升或降低多少?
(3)若企业每件一等品售价180元,每件二等品售价150元,每件三等品售价120元,以样本中的频率代替相应概率,现有一名顾客随机购买两件产品,设其支付的费用为X(单位:元),求X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列有关命题的说法正确的是( )
A.命题“若![]() ⊥
⊥![]() ,则
,则![]()
![]() 0”的否命题为“若
0”的否命题为“若![]() ⊥
⊥![]() ,则
,则![]()
![]() 0”
0”
B.命题“函数f(x)=(a﹣1)x是R上的增函数”的否定是“函数f(x)=(a﹣1)x是R上的减函数”
C.命题“在△ABC中,若sinA=sinB,则A=B”的逆否命题为真命题
D.命题“若x=2,则x2﹣3x+2=0”的逆命题为真命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,将曲线
,将曲线![]() 向左平移
向左平移![]() 个单位长度得到曲线
个单位长度得到曲线![]() .
.
(1)求曲线![]() 的参数方程;
的参数方程;
(2)已知![]() 为曲线
为曲线![]() 上的动点,
上的动点, ![]() 两点的极坐标分别为
两点的极坐标分别为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国仓储指数是反映仓储行业经营和国内市场主要商品供求状况与变化趋势的已套指数体系.如图所示的折线图是2017年和2018年的中国仓储指数走势情况.根据该折线图,下列结论中不正确的是( )
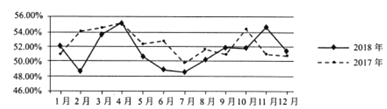
A. 2018年1月至4月的仓储指数比2017年同期波动性更大
B. 这两年的最大仓储指数都出现在4月份
C. 2018年全年仓储指数平均值明显低于2017年
D. 2018年各仓储指数的中位数与2017年各仓储指数中位数差异明显
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了变废为宝,节约资源,新上了一个从生活垃圾中提炼生物柴油的项目.经测算该项目月处理成本![]() (元)与月处理量
(元)与月处理量![]() (吨)之间的函数关系可以近似地表示为:
(吨)之间的函数关系可以近似地表示为:
 ,且每处理一吨生活垃圾,可得到能利用的生物柴油价值为200元,若该项目不获利,政府将给予补贴.
,且每处理一吨生活垃圾,可得到能利用的生物柴油价值为200元,若该项目不获利,政府将给予补贴.
(1)当![]() 时,判断该项目能否获利?如果获利,求出最大利润;如果不获利,则政府每月至少需要补贴多少元才能使该项目不亏损?
时,判断该项目能否获利?如果获利,求出最大利润;如果不获利,则政府每月至少需要补贴多少元才能使该项目不亏损?
(2)该项目每月处理量为多少吨时,才能使每吨的平均处理成本最低?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】朱世杰是元代著名数学家,他所著《算学启蒙》是一部在中国乃至世界最早的科学普及著作.《算学启蒙》中提到一些堆垛问题,如“三角垛果子”,就是将一样大小的果子堆垛成正三棱锥,每层皆堆成正三角形,从上向下数,每层果子数分别为1,3,6,10,…,现有一个“三角垛果子”,其最底层每边果子数为10,则该层果子数为( )
A. 50B. 55C. 100D. 110
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com