
【题目】已知函数f(x)= ![]() (其中e是自然对数的底数,a∈R). (Ⅰ)若曲线f(x)在x=l处的切线与x轴不平行,求a的值;
(其中e是自然对数的底数,a∈R). (Ⅰ)若曲线f(x)在x=l处的切线与x轴不平行,求a的值;
(Ⅱ)若函数f(x)在区间(0,1]上是单调函数,求a的最大值.
【答案】解:(Ⅰ)依题意,f′(x)= 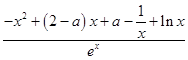 , f′(1)=0,且曲线f(x)在x=1处的切线方程为y=
, f′(1)=0,且曲线f(x)在x=1处的切线方程为y= ![]() ,
,
∵切线与x轴不平行,故切线与x轴重合,∴ ![]() ,即a=﹣1;
,即a=﹣1;
(Ⅱ)f′(x)= 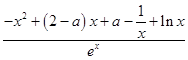 ,
,
设h(x)= ![]() ,则h′(x)=﹣2x+(2﹣a)+
,则h′(x)=﹣2x+(2﹣a)+ ![]() .
.
h′(x)在(0,1]上是减函数,从而h′(x)>h′(1)=2﹣a.
①当2﹣a≥0,即a≤2时,h′(x)≥0,h(x)在区间(0,1)上为增函数.
∵h(1)=0,∴h(x)≤0在(0,1]上恒成立,即f′(x)≤0在(0,1]上恒成立.
∴f(x)在(0,1]上是减函数.
∴a≤2满足题意;
②当2﹣a<0,即a>2时,设函数h′(x)的唯一零点为x1 ,
则h(x)在(0,x1)上递增,在(x1 , 1)上递减.
又∵h(1)=0,∴h(x1)>0.
又∵h(e﹣a)=﹣e﹣2a+(2﹣a)e﹣a+a﹣ea+lne﹣a=﹣e﹣2a+(2﹣a)e﹣a﹣ea<0,
∴h(x)在(0,1)内由唯一一个零点x′,
当x∈(0,x′)时,h(x)<0,当x∈(x′,1)时,h(x)>0.
从而f(x)在(0,x′)上递减,在(x′,1)上递增,与在区间(0,1]上是单调函数矛盾.
∴a>2不合题意.
综上,a的最大值为2.
【解析】(Ⅰ)求出原函数的导函数,可得f′(1)=0,得到曲线f(x)在x=1处的切线方程为y= ![]() ,结合切线与x轴不平行,可得
,结合切线与x轴不平行,可得 ![]() ,从而求得a值;(Ⅱ)由f′(x)=
,从而求得a值;(Ⅱ)由f′(x)= ![]() ,设h(x)=
,设h(x)= ![]() ,求出h′(x),可知h′(x)在(0,1]上是减函数,从而h′(x)>h′(1)=2﹣a. 然后分当2﹣a≥0,和2﹣a<0分类研究函数的单调性得答案.
,求出h′(x),可知h′(x)在(0,1]上是减函数,从而h′(x)>h′(1)=2﹣a. 然后分当2﹣a≥0,和2﹣a<0分类研究函数的单调性得答案.
【考点精析】认真审题,首先需要了解利用导数研究函数的单调性(一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减).
在这个区间单调递减).


 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣m|(m>0),g(x)=2f(x)﹣f(x+m),g(x)的最小值为﹣1. (Ⅰ)求m的值;
(Ⅱ)若|a|<m,|b|<m,且a≠0.求证:f(ab)>|a|f( ![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an},其前n项和Sn=﹣3n2 , {bn}为单调递增的等比数列,b1b2b3=512,a1+b1=a3+b3 .
(1)求数列{an},{bn}的通项;
(2)若cn= ![]() ,数列{cn}的前n项和Tn , 求证:
,数列{cn}的前n项和Tn , 求证: ![]() <1.
<1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线C以F1(﹣2,0)、F2(2,0)为焦点,且过点P(7,12).
(1)求双曲线C与其渐近线的方程;
(2)若斜率为1的直线l与双曲线C相交于A,B两点,且 ![]() (O为坐标原点).求直线l的方程.
(O为坐标原点).求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数h(x)=ax3﹣1(a∈R),g(x)=lnx,f(x)=h(x)+3xg(x)(e为自然对数的底数).
(I)若f(x)图象过点(1,﹣1),求f(x)的单调区间;
(II)若f(x)在区间( ![]() ,e)上有且只有一个极值点,求实数a的取值范围;
,e)上有且只有一个极值点,求实数a的取值范围;
(III)函数F(x)=(a﹣ ![]() )x3+
)x3+ ![]() x2g(a)﹣h(x)﹣1,当a>e
x2g(a)﹣h(x)﹣1,当a>e ![]() 时,函数F(x)过点A(1,m)的切线至少有2条,求实数m的值.
时,函数F(x)过点A(1,m)的切线至少有2条,求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:函数f(x)=lg(ax2﹣ax+1)的定义域是R;命题 ![]() 在第一象限为增函数,若“p∧q”为假,“p∨q”为真,求a的取值范围.
在第一象限为增函数,若“p∧q”为假,“p∨q”为真,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com