
ЁОЬтФПЁПЁАЖтЛ§ЪѕЁБЪЧЮвЙњЙХДњЪ§бЇЕФживЊГЩОЭжЎвЛ.ФЯЫЮЪ§бЇМвбюЛддкЁЖЯъНтОХеТЫуЗЈЁЗжаМЧдиСЫЁАЗНЖтЁБЕФМЦЫуЗНЗЈЃКЁАЙћзгвдЖтЃЌЯТЗНЪЎЫФИіЃЌЮЪМЦМИКЮЃПЪѕдЛЃКЯТЗНМгвЛЃЌГЫЯТЗНЮЊЦНЛ§.гжМгАыЮЊИпЃЌвдГЫЯТЗНЮЊИпЛ§.ШчШ§ЖјвЛ.ЁБвтЫМЪЧЫЕЃЌНЋЙћзгвдЗНЖтЕФаЮЪНАкЗХЃЈЗНЖтМДУПВуОљЮЊе§ЗНаЮЃЌздЯТЖјЩЯУПВуУПБпЙћзгЪ§вРДЮЕнМѕ1ИіЃЌзюЩЯВуЮЊ1ИіЃЉЃЌзюЯТВуУПБпЙћзгЪ§ЮЊ14ИіЃЌЮЪЙВгаЖрЩйИіЙћзгЃПМЦЫуЗНЗЈгУЫуЪНБэЪОЮЊ![]() .РћгУЁАЗНЖтЁБЕФМЦЫуЗНЗЈЃЌПЩМЦЫузюЯТВуУПБпЙћзгЪ§ЮЊ14ИіЕФЁАШ§НЧЖтЁБЃЈШ§НЧЖтМДУПВуОљЮЊе§Ш§НЧаЮЃЌздЯТЖјЩЯУПВуУПБпЙћзгЪ§вРДЮЕнМѕ1ИіЃЌзюЩЯВуЮЊ1ИіЃЉЙВгаЙћзгЪ§ЮЊЃЈ ЃЉ
.РћгУЁАЗНЖтЁБЕФМЦЫуЗНЗЈЃЌПЩМЦЫузюЯТВуУПБпЙћзгЪ§ЮЊ14ИіЕФЁАШ§НЧЖтЁБЃЈШ§НЧЖтМДУПВуОљЮЊе§Ш§НЧаЮЃЌздЯТЖјЩЯУПВуУПБпЙћзгЪ§вРДЮЕнМѕ1ИіЃЌзюЩЯВуЮЊ1ИіЃЉЙВгаЙћзгЪ§ЮЊЃЈ ЃЉ
A.420ИіB.560ИіC.680ИіD.1015Иі
ЁОД№АИЁПB
ЁОНтЮіЁП
гЩЬтвтПЩЕУЃЌзюЯТВуУПБпЮЊ![]() ИіЙћзгЕФЁАЗНЖтЁБзмЕФЙћзгЪ§ЕФМЦЫуЪНЮЊ
ИіЙћзгЕФЁАЗНЖтЁБзмЕФЙћзгЪ§ЕФМЦЫуЪНЮЊ![]() ЃЌдйгЩзюЯТВуУПБпЮЊ
ЃЌдйгЩзюЯТВуУПБпЮЊ![]() ИіЙћзгЕФЁАШ§НЧВйЁБздЩЯЖјЯТЕФЕк
ИіЙћзгЕФЁАШ§НЧВйЁБздЩЯЖјЯТЕФЕк![]() ВуЙћзгЪ§ЮЊ
ВуЙћзгЪ§ЮЊ![]() ЃЌЕУ
ЃЌЕУ![]() ВуЁАШ§НЧВйЁБзмЕФЙћзгЪ§ЮЊ
ВуЁАШ§НЧВйЁБзмЕФЙћзгЪ§ЮЊ![]() ЃЌзюКѓгУЗжзщЧѓКЭЕФЗНЗЈМДПЩЧѓНт.
ЃЌзюКѓгУЗжзщЧѓКЭЕФЗНЗЈМДПЩЧѓНт.
гЩЬтвтжЊЃЌзюЯТВуУПБпЮЊ14ИіЙћзгЕФЁАЗНЖтЁБзмЕФЙћзгЪ§ЕФМЦЫуЪНЮЊ![]() ЃЌ
ЃЌ
ЫљвдПЩЕУзюЯТВуУПБпЮЊ![]() ИіЙћзгЕФЁАЗНЖтЁБзмЕФЙћзгЪ§ЕФМЦЫуЪНЮЊ
ИіЙћзгЕФЁАЗНЖтЁБзмЕФЙћзгЪ§ЕФМЦЫуЪНЮЊ![]() ЃЌ
ЃЌ
зюЯТВуУПБпЮЊ![]() ИіЙћзгЕФЁАШ§НЧЖтЁБздЩЯЖјЯТЕФЕк
ИіЙћзгЕФЁАШ§НЧЖтЁБздЩЯЖјЯТЕФЕк![]() ВуЙћзгЪ§ЮЊ
ВуЙћзгЪ§ЮЊ![]() ЃЌЫљвд
ЃЌЫљвд![]() ВуЁАШ§НЧЖтЁБзмЕФЙћзгЪ§ЮЊ
ВуЁАШ§НЧЖтЁБзмЕФЙћзгЪ§ЮЊ![]() ЃЌвђЮЊ
ЃЌвђЮЊ
![]()
![]()
![]()
![]()
![]() ЃЌ
ЃЌ
ЫљвдШЁ![]() ЃЌПЩЕУЁАШ§НЧЖтЁБЕФЙћзгзмЪ§ЮЊ560Иі.
ЃЌПЩЕУЁАШ§НЧЖтЁБЕФЙћзгзмЪ§ЮЊ560Иі.
ЙЪбЁЃКB



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНЋКЏЪ§![]() ЭМЯѓЩЯЕФИїЕуЕФКсзјБъЫѕЖЬЕНдРДЕФ
ЭМЯѓЩЯЕФИїЕуЕФКсзјБъЫѕЖЬЕНдРДЕФ![]() ЃЌзнзјБъВЛБфЃЌдйЯђзѓЦНвЦ
ЃЌзнзјБъВЛБфЃЌдйЯђзѓЦНвЦ![]() ИіЕЅЮЛЃЌЕУЕН
ИіЕЅЮЛЃЌЕУЕН![]() ЕФЭМЯѓЃЌЯТСаЫЕЗЈе§ШЗЕФЪЧЃЈ ЃЉ
ЕФЭМЯѓЃЌЯТСаЫЕЗЈе§ШЗЕФЪЧЃЈ ЃЉ
A.Еу![]() ЪЧКЏЪ§
ЪЧКЏЪ§![]() ЭМЯѓЕФЖдГЦжааФ
ЭМЯѓЕФЖдГЦжааФ
B.КЏЪ§![]() дк
дк![]() ЩЯЕЅЕїЕнМѕ
ЩЯЕЅЕїЕнМѕ
C.КЏЪ§![]() ЕФЭМЯѓгыКЏЪ§
ЕФЭМЯѓгыКЏЪ§![]() ЕФЭМЯѓЯрЭЌ
ЕФЭМЯѓЯрЭЌ
D.Шє![]() ЃЌ
ЃЌ![]() ЪЧКЏЪ§ЕФСуЕуЃЌдђ
ЪЧКЏЪ§ЕФСуЕуЃЌдђ![]() ЪЧ
ЪЧ![]() ЕФећЪ§БЖ
ЕФећЪ§БЖ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЙЋЫОвдПЭЛЇТњвтЮЊГіЗЂЕуЃЌЫцЛњГщбЁ2000УћПЭЛЇЃЌвдЕїВщЮЪОэЕФаЮЪНЗжЮігАЯьПЭЛЇТњвтЖШЕФИїЯювђЫиЃЎУПУћПЭЛЇЬюаДвЛИівђЫиЃЌЯТЭМЮЊПЭЛЇТњвтЖШЗжЮіЕФХСРлЭаЭМЃЎХСРлЭаЭМгУЫЋжБНЧзјБъЯЕБэЪОЃЌзѓБпзнзјБъБэЪОЦЕЪ§ЃЌгвБпзнзјБъБэЪОЦЕТЪЃЌЗжЮіЯпБэЪОРлМЦЦЕТЪЃЌКсзјБъБэЪОгАЯьТњвтЖШЕФИїЯювђЫиЃЌАДгАЯьГЬЖШЃЈМДЦЕЪ§ЃЉЕФДѓаЁДгзѓЕНгвХХСаЃЌвдЯТНсТле§ШЗЕФИіЪ§ЪЧЃЈ ЃЉЃЎ
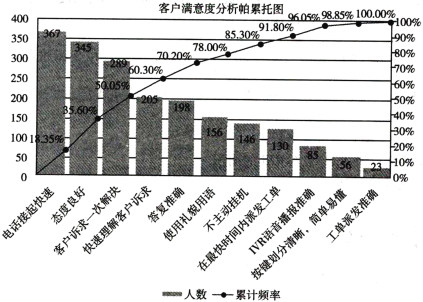
Ђй35.6%ЕФПЭЛЇШЯЮЊЬЌЖШСМКУгАЯьЫћУЧЕФТњвтЖШЃЛ
Ђк156ЮЛПЭЛЇШЯЮЊЪЙгУРёУВгУгягАЯьЫћУЧЕФТњвтЖШЃЛ
ЂлзюгАЯьПЭЛЇТњвтЖШЕФвђЫиЪЧЕчЛАНгЦ№ПьЫйЃЛ
ЂмВЛГЌЙ§10%ЕФПЭЛЇШЯЮЊЙЄЕЅХЩЗЂзМШЗгАЯьЫћУЧЕФТњвтЖШЃЎ
A.1B.2C.3D.4
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊ![]() ЮЊзјБъдЕуЃЌХзЮяЯп
ЮЊзјБъдЕуЃЌХзЮяЯп![]() ЕФНЙЕузјБъЮЊ
ЕФНЙЕузјБъЮЊ![]() ЃЌЕу
ЃЌЕу![]() ЃЌ
ЃЌ![]() дкИУХзЮяЯпЩЯЧвЮЛгк
дкИУХзЮяЯпЩЯЧвЮЛгк![]() жсЕФСНВрЃЌ
жсЕФСНВрЃЌ![]() ЃЎ
ЃЎ
ЃЈЂёЃЉжЄУїЃКжБЯп![]() Й§ЖЈЕу
Й§ЖЈЕу![]() ЃЛ
ЃЛ
ЃЈЂђЃЉвд![]() ЃЌ
ЃЌ![]() ЮЊЧаЕузї
ЮЊЧаЕузї![]() ЕФЧаЯпЃЌЩшСНЧаЯпЕФНЛЕуЮЊ
ЕФЧаЯпЃЌЩшСНЧаЯпЕФНЛЕуЮЊ![]() ЃЌЕу
ЃЌЕу![]() ЮЊдВ
ЮЊдВ![]() ЩЯШЮвтвЛЕуЃЌЧѓ
ЩЯШЮвтвЛЕуЃЌЧѓ![]() ЕФзюаЁжЕЃЎ
ЕФзюаЁжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПКЏЪ§![]() .
.
ЃЈ1ЃЉЕБ![]() ЪБЃЌЬжТлКЏЪ§
ЪБЃЌЬжТлКЏЪ§![]() ЕФЕЅЕїадЃЛ
ЕФЕЅЕїадЃЛ
ЃЈ2ЃЉЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЪБЃЌ
ЪБЃЌ![]() КуГЩСЂЃЌЧѓе§ећЪ§
КуГЩСЂЃЌЧѓе§ећЪ§![]() ЕФзюДѓжЕ.
ЕФзюДѓжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЖрУцЬх![]() жаЃЌ
жаЃЌ![]() СНСНДЙжБЃЌЫФБпаЮ
СНСНДЙжБЃЌЫФБпаЮ![]() ЪЧБпГЄЮЊ2ЕФе§ЗНаЮЃЌAC
ЪЧБпГЄЮЊ2ЕФе§ЗНаЮЃЌAC![]() DG
DG![]() EFЃЌЧв
EFЃЌЧв![]() .
.
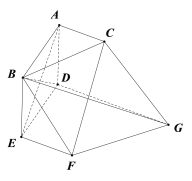
ЃЈ1ЃЉжЄУїЃК![]() ЦНУц
ЦНУц![]() .
.
ЃЈ2ЃЉЧѓЖўУцНЧ![]() ЕФгрЯвжЕ.
ЕФгрЯвжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() ЃЌ
ЃЌ![]() ЃЌmЃЌn
ЃЌmЃЌn![]() R.
R.
ЃЈ1ЃЉЕБmЃН0ЪБЃЌЧѓКЏЪ§![]() ЕФМЋжЕЃЛ
ЕФМЋжЕЃЛ
ЃЈ2ЃЉЕБnЃН0ЪБЃЌКЏЪ§![]() дк(0ЃЌ
дк(0ЃЌ![]() )ЩЯЮЊЕЅЕїКЏЪ§ЃЌЧѓmЕФШЁжЕЗЖЮЇЃЛ
)ЩЯЮЊЕЅЕїКЏЪ§ЃЌЧѓmЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉЕБnЃО0ЪБЃЌХаЖЯЪЧЗёДцдке§Ъ§mЃЌЪЙЕУКЏЪ§![]() гы
гы![]() гаЯрЭЌЕФСуЕуЃЌВЂЫЕУїРэгЩ.
гаЯрЭЌЕФСуЕуЃЌВЂЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЫЋЧњЯпCЃК![]() 1ЃЈaЃО0ЃЌbЃО0ЃЉЕФзѓНЙЕуЮЊFЃЈЉcЃЌ0ЃЉЃЌХзЮяЯпy2ЃН4cxЕФзМЯпгыЫЋЧњЯпЕФвЛИіНЛЕуЮЊPЃЌЕуMЮЊЯпЖЮPFЕФжаЕуЃЌЧвЁїOFMЮЊЕШбќжБНЧШ§НЧаЮЃЌдђЫЋЧњЯпCЕФРыаФТЪЮЊЃЈ ЃЉ
1ЃЈaЃО0ЃЌbЃО0ЃЉЕФзѓНЙЕуЮЊFЃЈЉcЃЌ0ЃЉЃЌХзЮяЯпy2ЃН4cxЕФзМЯпгыЫЋЧњЯпЕФвЛИіНЛЕуЮЊPЃЌЕуMЮЊЯпЖЮPFЕФжаЕуЃЌЧвЁїOFMЮЊЕШбќжБНЧШ§НЧаЮЃЌдђЫЋЧњЯпCЕФРыаФТЪЮЊЃЈ ЃЉ
A.![]() B.
B.![]() 1C.
1C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕxoyжаЃЌвдзјБъдЕуЮЊМЋЕуЃЌxжсе§АыжсЮЊМЋжсНЈСЂМЋзјБъЯЕЃЌЧњЯпEЕФМЋзјБъЗНГЬЮЊ![]() ЃЌжБЯпlЕФВЮЪ§ЗНГЬЮЊ
ЃЌжБЯпlЕФВЮЪ§ЗНГЬЮЊ![]() (tЮЊВЮЪ§).ЕуPЮЊЧњЯпEЩЯЕФЖЏЕуЃЌЕуQЮЊЯпЖЮOPЕФжаЕу.
(tЮЊВЮЪ§).ЕуPЮЊЧњЯпEЩЯЕФЖЏЕуЃЌЕуQЮЊЯпЖЮOPЕФжаЕу.
ЃЈ1ЃЉЧѓЕуQЕФЙьМЃ(ЧњЯпC)ЕФжБНЧзјБъЗНГЬЃЛ
ЃЈ2ЃЉШєжБЯпlНЛЧњЯпCгкAЃЌBСНЕуЃЌЕу![]() ЧЁКУЮЊЯпЖЮABЕФШ§ЕШЗжЕуЃЌЧѓжБЯпlЕФЦеЭЈЗНГЬ.
ЧЁКУЮЊЯпЖЮABЕФШ§ЕШЗжЕуЃЌЧѓжБЯпlЕФЦеЭЈЗНГЬ.
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com