
【题目】已知函数![]()
(1)当a=-2时,求函数f(x)的极值;
(2)若ln[e(x+1)]≥2- f(-x)对任意的x∈[0,+∞)成立,求实数a的取值范围.
科目:高中数学 来源: 题型:
【题目】山东省2020年高考将实施新的高考改革方案.考生的高考总成绩将由3门统一高考科目成绩和自主选择的3门普通高中学业水平等级考试科目成绩组成,总分为750分.其中,统一高考科目为语文、数学、外语,自主选择的3门普通高中学业水平等级考试科目是从物理、化学、生物、历史、政治、地理6科中选择3门作为选考科目,语、数、外三科各占150分,选考科目成绩采用“赋分制”,即原始分数不直接用,而是按照学生分数在本科目考试的排名来划分等级并以此打分得到最后得分.根据高考综合改革方案,将每门等级考试科目中考生的原始成绩从高到低分为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 共8个等级。参照正态分布原则,确定各等级人数所占比例分别为
共8个等级。参照正态分布原则,确定各等级人数所占比例分别为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() .等级考试科目成绩计入考生总成绩时,将
.等级考试科目成绩计入考生总成绩时,将![]() 至
至![]() 等级内的考生原始成绩,依照等比例转换法则,分别转换到91-100、81-90、71-80,61-70、51-60、41-50、31-40、21-30八个分数区间,得到考生的等级成绩.
等级内的考生原始成绩,依照等比例转换法则,分别转换到91-100、81-90、71-80,61-70、51-60、41-50、31-40、21-30八个分数区间,得到考生的等级成绩.
举例说明.
某同学化学学科原始分为65分,该学科![]() 等级的原始分分布区间为58~69,则该同学化学学科的原始成绩属
等级的原始分分布区间为58~69,则该同学化学学科的原始成绩属![]() 等级.而
等级.而![]() 等级的转换分区间为61~70,那么该同学化学学科的转换分为:
等级的转换分区间为61~70,那么该同学化学学科的转换分为:
设该同学化学科的转换等级分为![]() ,
,![]() ,求得
,求得![]() .
.
四舍五入后该同学化学学科赋分成绩为67.
(1)某校高一年级共2000人,为给高一学生合理选科提供依据,对六个选考科目进行测试,其中物理考试原始成绩基本服从正态分布![]() .
.
(i)若小明同学在这次考试中物理原始分为84分,等级为![]() ,其所在原始分分布区间为82~93,求小明转换后的物理成绩;
,其所在原始分分布区间为82~93,求小明转换后的物理成绩;
(ii)求物理原始分在区间![]() 的人数;
的人数;
(2)按高考改革方案,若从全省考生中随机抽取4人,记![]() 表示这4人中等级成绩在区间
表示这4人中等级成绩在区间![]() 的人数,求
的人数,求![]() 的分布列和数学期望.
的分布列和数学期望.
(附:若随机变量![]() ,则
,则![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】港珠澳大桥是一座具有划时代意义的大桥.它连通了珠海、香港、澳门三地,大大缩短了三地的时空距离,盘活了珠江三角洲的经济,被誉为新的世界七大奇迹.截至2019年10月23日8点,珠海公路口岸共验放出入境旅客超过1400万人次,日均客流量已经达到4万人次,验放出入境车辆超过70万辆次,2019年春节期间,客流再次大幅增长,日均客流达8万人次,单日客流量更是创下11.3万人次的最高纪录.2019年从五月一日开始的连续100天客流量频率分布直方图如图.
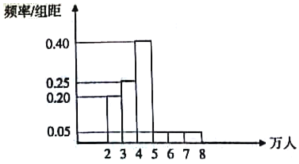
(1)求这100天中,客流量超过4万的频率;
(2)①同一组数据用该区间的中点值代替,根据频率分布直方图.估计客流量的平均数.
②求客流量的中位数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在统计学中,同比增长率一般是指和去年同期相比较的增长率,环比增长率一般是指和前一时期相比较的增长率.2020年2月29日人民网发布了我国2019年国民经济和社会发展统计公报图表,根据2019年居民消费价格月度涨跌幅度统计折线图,下列说法正确的是( )
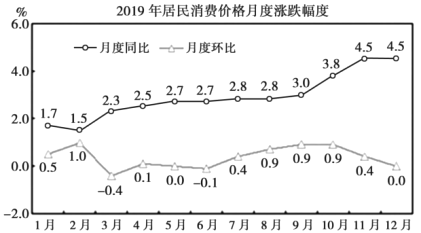
A.2019年我国居民每月消费价格与2018年同期相比有涨有跌
B.2019年我国居民每月消费价格中2月消费价格最高
C.2019年我国居民每月消费价格逐月递增
D.2019年我国居民每月消费价格3月份较2月份有所下降
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若实数![]() 满足
满足![]() ,则称
,则称![]() 为函数
为函数![]() 的不动点.
的不动点.
(1)求函数![]() 的不动点;
的不动点;
(2)设函数![]() ,其中
,其中![]() 为实数.
为实数.
① 若![]() 时,存在一个实数
时,存在一个实数![]() ,使得
,使得![]() 既是
既是![]() 的不动点,又是
的不动点,又是![]() 的不动点(
的不动点(![]() 是函数
是函数![]() 的导函数),求实数
的导函数),求实数![]() 的取值范围;
的取值范围;
② 令![]() ,若存在实数
,若存在实数![]() ,使
,使![]() ,
,![]() ,
,![]() ,
,![]() 成各项都为正数的等比数列,求证:函数
成各项都为正数的等比数列,求证:函数![]() 存在不动点.
存在不动点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com