
已知函数f(x)=2sin(ωx),其中常数ω>0
(1)令ω=1,判断函数F(x)=f(x)+f(x+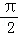 )的奇偶性,并说明理由;
)的奇偶性,并说明理由;
(2)令ω=2,将函数y=f(x)的图象向左平移个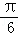 单位,再向上平移1个单位,得到函数y=g(x)的图象,对任意a∈R,求y=g(x)在区间[a,a+10π]上零点个数的所有可能值.
单位,再向上平移1个单位,得到函数y=g(x)的图象,对任意a∈R,求y=g(x)在区间[a,a+10π]上零点个数的所有可能值.
(1)F(x)既不是奇函数,也不是偶函数(2)21或20
【解析】
试题分析:(1)f(x)=2sinx,
F(x)=f(x)+f(x+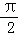 )=2sinx+2sin(x+
)=2sinx+2sin(x+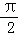 )=2(sinx+cosx),
)=2(sinx+cosx),
F(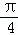 )=2
)=2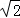 ,F(﹣
,F(﹣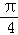 )=0,F(﹣
)=0,F(﹣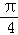 )≠F(
)≠F(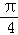 ),F(﹣
),F(﹣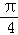 )≠﹣F(
)≠﹣F(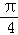 ),
),
所以,F(x)既不是奇函数,也不是偶函数.
(2)f(x)=2sin2x,
将y=f(x)的图象向左平移 个单位,再向上平移1个单位后得到y=2sin2(x+
个单位,再向上平移1个单位后得到y=2sin2(x+ )+1的图象,所以g(x)=2sin2(x+
)+1的图象,所以g(x)=2sin2(x+ )+1.
)+1.
令g(x)=0,得x=kπ+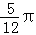 或x=kπ+
或x=kπ+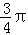 (k∈z),
(k∈z),
因为[a,a+10π]恰含10个周期,所以,当a是零点时,在[a,a+10π]上零点个数21,
当a不是零点时,a+kπ(k∈z)也都不是零点,区间[a+kπ,a+(k+1)π]上恰有两个零点,故在[a,a+10π]上有20个零点.
综上,y=g(x)在[a,a+10π]上零点个数的所有可能值为21或20.
考点:函数y=Asin(ωx+φ)的图象变换;函数奇偶性的判断;根的存在性及根的个数判断
点评:本题考查函数y=Asin(ωx+φ)的图象变换、函数的奇偶性、根的存在性及根的个数的判断,考查数形结合思想,结合图象分析是解决(2)问的关键


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:高中数学 来源: 题型:
| 1 |
| x |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com