
����Ŀ��ij��ѧ�հ�Ǩ����У����ѧУ���ǣ�����סУ����ѧ·�ϵ�������ʱ���˾�����20���ӣ���ѧУ�Ƴ�5�����ϿΣ�Ϊ�ˣ�У�������ȡ100����סУ������������ѧ·�ϵ�������ʱ�䣨��λ�����ӣ��������������ݻ��Ƴ�����Ƶ�ʷֲ�ֱ��ͼ������ʱ�����Ϊ[0��10����[10��20����[20��30����[30��40����[40��50]�� 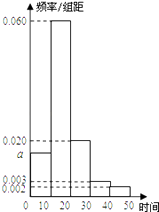
��1����Ƶ�ʷֲ�ֱ��ͼ��a��ֵ��
��2����ͳ��ѧ�ĽǶ�˵��ѧУ�Ƿ���Ҫ�Ƴ�5�����ϿΣ�
��3��������������ʱ�䲻С��30���ӵ�ѧ���У������ȡ2�ˣ���ǡ��һ��ѧ���ĵ���ʱ������[40��50]�ϵĸ��ʣ�
���𰸡�
��1���⣺ʱ�����Ϊ[0��10����Ƶ��Ϊ
1��10��0.06+0.02+0��003+0.002��=0.15��
��a= ![]() =0.015��
=0.015��
���������Ƶ��ֱ��ͼ��a��ֵΪ0.015��
��2���⣺100����סУ����ѧ·�ϵ�������ʱ���ƽ������
![]() =0.15��5+0.6��15+0.2��25+0.03��35+0.02��45=16.7��
=0.15��5+0.6��15+0.2��25+0.03��35+0.02��45=16.7��
��Ϊ16.7��20��
���Ը�У����Ҫ�Ƴ�5�����ϿΣ�
��3���⣺���������������ĵ�������ʱ����[30��40���е���3�ˣ�������Ϊa��b��c��
��������ʱ����[40��50���е���2�ˣ�������ΪA��B��
�ӵ�������ʱ�䲻С��30���ӵ�5��ѧ���У������ȡ2�˹�������10�������
��a��b������a��c������a��A������a��B������b��c������b��A������b��B������c��A������c��B������A��B������ǡ��һ��ѧ���ĵ�������ʱ������[40��50]�е�������6�֣�
��a��A������a��B������b��A������b��B������c��A������c��B����
��ǡ��һ��ѧ���ĵ�������ʱ������[40��50]�еĸ���P= ![]() =
= ![]()
��������������Ƶ�ʷֲ�ֱ��ͼ�������֮��Ϊ1�������ֱ��ͼ�е�a��ֵ�������������ѧ����ʱ���ƽ��ֵ������20�Ƚϼ��ɵõ��𰸣������ݷֲ����ȷ��[30��40����[40��50����ȡ���������о������ȡ���˵Ļ����¼����ҳ�ǡ��һ��ѧ���ĵ���ʱ������[40��50]���¼������Ļ����¼������ø��ʹ�ʽ���㼴�ɣ�
�����㾫��������Ƶ�ʷֲ�ֱ��ͼ����Ŀ�����жϼ��ɵõ��𰸣���Ҫ��֪Ƶ�ʷֲ�����Ƶ�ʷֲ�ֱ��ͼ���Ƕ���ͬ���ݵ����ֲ�ͬ���﷽ʽ.�ý��յı���ı����ݵ����з�ʽ������ʽ����չʾ���ݵķֲ����.ͨ����ͼ�ȿ��Դ���������ȡ��Ϣ���ֿ�������ͼ�δ�����Ϣ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������{an}����a1=a��an+1=can+1��c��n��N*��������a��cΪʵ������c��0�� ����������{an}��ͨ�ʽ��
������ ![]() ��������{bn}��ǰn���Sn ��
��������{bn}��ǰn���Sn ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪f��x��=3x2��2x������{an}��ǰn���ΪSn �� �㣨n��Sn����n��N*�����ں���y=f��x����ͼ���ϣ�
��1��������{an}��ͨ�ʽ��
��2����bn= ![]() ��Tn������{bn}��ǰn��ͣ���ʹ��Tn��
��Tn������{bn}��ǰn��ͣ���ʹ��Tn�� ![]() ������n��N*����������С������m��
������n��N*����������������m��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ����װ�и�ɫ��12ֻ������5������4������2������1�����������ȡ��1����
��1��ȡ����1���Ǻ�������ĸ��ʣ�
��2��ȡ����1���Ǻ�����������ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��A���� ![]() ��0����B��
��0����B�� ![]() ��0��������E����ֱ��EA��ֱ��EB��б��֮��Ϊ��
��0��������E����ֱ��EA��ֱ��EB��б��֮��Ϊ�� ![]() ��
��
��1����E�Ĺ켣C�ķ��̣�
��2�������F��1��0����ֱ��l1������C���ڵ�P��Q���ǵ�P��ֱ��l2��x=2�ľ���Ϊd�� 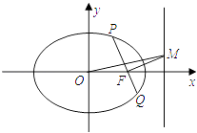
�������� ![]() ��ֵ��
��ֵ��
����������F��ֱ��l1�Ĵ��߽�ֱ��l2�ڵ�M����֤��ֱ��OMƽ���߶�PQ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=lnx�� ![]() a��x��1����a��R����
a��x��1����a��R����
��1����a=��2��������y=f��x���ڵ㣨1��f��1�����������߷��̣�
��2��������ʽf��x����0������x�ʣ�1��+�ޣ�������� ��������ʵ��a��ȡֵ��Χ��
�������ԱȽ�ea��2��ae��2�Ĵ�С��������֤����eΪ��Ȼ�����ĵ�����e=2.71828����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��l1��x+my+6=0��l2����m��2��x+3y+2m=0����
��1����l1��l2 �� ��m��ֵ��
��2����l1��l2 �� ��m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У�ACƽ�֡�DAB����ABC=60�㣬AC=6��AD=5��S��ADC= ![]() ����AB�ij���
����AB�ij��� 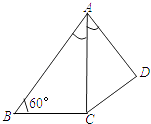
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com