
| t |
| 30 |
| A、5太贝克 |
| B、75In2太贝克 |
| C、150In2太贝克 |
| D、150太贝克 |
科目:高中数学 来源:2013届广东省高二第七学段考试理科数学试卷(解析版) 题型:选择题
放射性元素由于不断有原子放射出微粒子而变成其他元素,其含量不断减少,这种现象成为衰变,假设在放射性同位素铯137的衰变过程中,其含量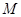 (单位:太贝克)与时间
(单位:太贝克)与时间 (单位:年)满足函数关系:
(单位:年)满足函数关系: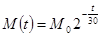 ,其中
,其中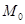 为
为 时铯137的含量,已知
时铯137的含量,已知 时,铯137的含量的变化率是
时,铯137的含量的变化率是 (太贝克/年),则
(太贝克/年),则 (
)
(
)
A. 5太贝克 B.  太贝克
太贝克
C.  太贝克 D. 150太贝克
太贝克 D. 150太贝克
查看答案和解析>>
科目:高中数学 来源:2013届陕西省高二上学期期末考试理科数学 题型:填空题
放射性元素由于不断有原子放射出微粒子而变成其他元素,其含量不断减少,这种现象成为衰变,假设在放射性同位素铯137的衰变过程中,其含量 (单位:太贝克)与时间
(单位:太贝克)与时间 (单位:年)满足函数关系:
(单位:年)满足函数关系: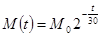 ,其中
,其中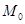 为
为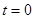 时铯137的含量,已知
时铯137的含量,已知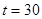 时,铯137的含量的变化率是
时,铯137的含量的变化率是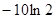 (太贝克/年),则
(太贝克/年),则 太贝克.
太贝克.
查看答案和解析>>
科目:高中数学 来源:2011年湖北省高考数学试卷(理科)(解析版) 题型:选择题
 ,其中M为t=0时铯137的含量.已知t=30时,铯137含量的变化率是-10In2(太贝克/年),则M(60)=( )
,其中M为t=0时铯137的含量.已知t=30时,铯137含量的变化率是-10In2(太贝克/年),则M(60)=( )查看答案和解析>>
科目:高中数学 来源: 题型:
放射性元素由于不断有原子放射出微粒子而变成其他元素,其含量不断减少,这种现象称为衰变。假设在放射性同位素铯137的衰变过程中,其含量M(单位:太贝克)与时间t(单位:年)满足函数关系:![]() ,其中M0为t=0时铯137的含量。已知t=30时,铯137含量的变化率是-10In2(太贝克/年),则M(60)=
,其中M0为t=0时铯137的含量。已知t=30时,铯137含量的变化率是-10In2(太贝克/年),则M(60)=
A.5太贝克 B.75In2太贝克
C.150In2太贝克 D.150太贝克
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com