
【题目】如图,在长方形ABCD中,AB=4,AD=2,点E是DC的中点,将△ADE沿AE折起,使平面ADE⊥平面ABCE,连结DB、DC、EB.
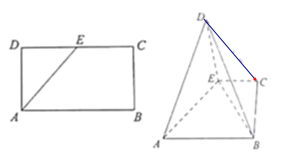
(1)求证:平面ADE⊥平面BDE;
(2)求AD与平面BDC所成角的正弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)利用勾股定理的逆定理可得:AE⊥EB,再利用面面垂直的判定定理即可得出:BE⊥平面ADE,进而证明结论.
(2)建立空间直角坐标系.设平面BDC的法向量为![]() ,可得
,可得![]() 求出
求出![]() ,可得AD与平面BDC所成角的正弦值
,可得AD与平面BDC所成角的正弦值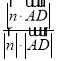 .
.
(1)证明:AE2+BE2![]() 16=AB2,∴AE⊥EB,
16=AB2,∴AE⊥EB,
又平面ADE⊥平面ABCE,平面ADE∩平面ABCE=AE,
∴BE⊥平面ADE,又![]() 平面
平面![]() ,
,
∴平面ADE⊥平面BDE;
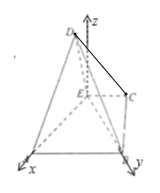
(2)解:如图所示,建立空间直角坐标系.E(0,0,0),A(2![]() ,0,0),B(0,2
,0,0),B(0,2![]() ,0),D(
,0),D(![]() ,0,
,0,![]() ),C(
),C(![]() ,
,![]() ,0).
,0).
![]() (
(![]() ,
,![]() ,0).
,0).![]() (
(![]() ,2
,2![]() ,
,![]() ),
),![]() (
(![]() ,0,
,0,![]() ),
),
设平面BDC的法向量为![]()
则![]() ,
,![]() ,
,![]() x+2
x+2![]() z=0,
z=0,
取![]() .
.
∴AD与平面BDC所成角的正弦值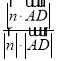
![]() .
.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源: 题型:
【题目】某校高二年级某班的数学课外活动小组有6名男生,4名女生,从中选出4人参加数学竞赛考试,用X表示其中男生的人数.
(1)请列出X的分布列;
(2)根据你所列的分布列求选出的4人中至少有3名男生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】依据某地某条河流8月份的水文观测点的历史统计数据所绘制的频率分布直方图如图(甲)所示;依据当地的地质构造,得到水位与灾害等级的频率分布条形图如图(乙)所示.
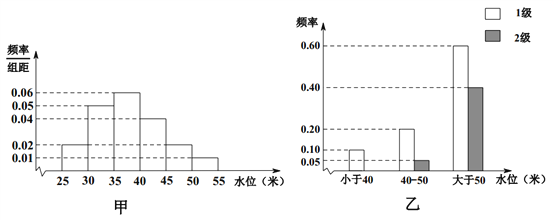
试估计该河流在8月份水位的中位数;
(1)以此频率作为概率,试估计该河流在8月份发生1级灾害的概率;
(2)该河流域某企业,在8月份,若没受1、2级灾害影响,利润为500万元;若受1级灾害影响,则亏损100万元;若受2级灾害影响则亏损1000万元.
现此企业有如下三种应对方案:
方案 | 防控等级 | 费用(单位:万元) |
方案一 | 无措施 | 0 |
方案二 | 防控1级灾害 | 40 |
方案三 | 防控2级灾害 | 100 |
试问,如仅从利润考虑,该企业应选择这三种方案中的哪种方案?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在①![]() .②
.②![]() 的面积
的面积![]() ,③
,③![]() 这三个条件中任选一个,补充在下面问题中,问题中的
这三个条件中任选一个,补充在下面问题中,问题中的![]() 是否为等边三角形,请说明理由.在
是否为等边三角形,请说明理由.在![]() 中,
中,![]() 分别为内角
分别为内角![]() 的对边,且
的对边,且![]() ,________,试判断
,________,试判断![]() 是否为等边三角形?(注:如果选择多个条件分别解答,按第一个解答计分)
是否为等边三角形?(注:如果选择多个条件分别解答,按第一个解答计分)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设点M是棱长为2的正方体ABCD-A1B1C1D1的棱AD的中点,点P在面BCC1B1所在的平面内,若平面D1PM分别与平面ABCD和平面BCC1B1所成的锐二面角相等,则点P到点C1的最短距离是( )
A.![]() B.
B.![]() C.1D.
C.1D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学生将语文、数学、英语、物理、化学、生物![]() 科的作业安排在周六、周日完成,要求每天至少完成两科,且数学、物理作业不在同一天完成,则完成作业的不同顺序种数为______.
科的作业安排在周六、周日完成,要求每天至少完成两科,且数学、物理作业不在同一天完成,则完成作业的不同顺序种数为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有关独立性检验的四个命题,其中正确的是( )
A.两个变量的2×2列联表中,对角线上数据的乘积相差越大,说明两个变量有关系成立的可能性就越大
B.对分类变量X与Y的随机变量![]() 的观测值k来说,k越小,“X与Y有关系”的可信程度越小
的观测值k来说,k越小,“X与Y有关系”的可信程度越小
C.从独立性检验可知:有95%的把握认为秃顶与患心脏病有关,我们说某人秃顶,那么他有95%的可能患有心脏病
D.从独立性检验可知:有99%的把握认为吸烟与患肺癌有关,是指在犯错误的概率不超过1%的前提下认为吸烟与患肺癌有关
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂加工产品![]() 的工人的年龄构成和相应的平均正品率如下表:
的工人的年龄构成和相应的平均正品率如下表:
年龄(单位:岁) |
|
|
|
|
人数比例 | 0.3 | 0.4 | 0.2 | 0.1 |
平均正品率 | 85% | 95% | 80% | 70% |
(1)画出该工厂加工产品![]() 的工人的年龄频率分布直方图;
的工人的年龄频率分布直方图;
(2)估计该工厂工人加工产品![]() 的平均正品率;
的平均正品率;
(3)该工厂想确定一个转岗年龄![]() 岁,到达这个年龄的工人不再加工产品
岁,到达这个年龄的工人不再加工产品![]() ,转到其他岗位,为了使剩余工人加工产品
,转到其他岗位,为了使剩余工人加工产品![]() 的平均正品率不低于90%,若年龄在同一区间内的工人加工产品
的平均正品率不低于90%,若年龄在同一区间内的工人加工产品![]() 的正品率都取相应区间的平均正品率,则估计
的正品率都取相应区间的平均正品率,则估计![]() 最高可定为多少岁?
最高可定为多少岁?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com