Question

【题目】如果一个多项式的系数都是自然数，则称为“自然多项式”.对正整数，用表示满足的不同自然多项式的个数.证明：.

Answer 1

【答案】见解析

【解析】

首先证明：对任何正整数，有. ①

事实上，对任何满足的自然多项式，因为奇数，所以，的常数项为奇数.令.则是自然多项式，且.

反之，对任何满足的自然多项式，令.则是自然多项式，且.

所以，.

对任何满足的自然多项式，若，令，则是自然多项式，且，这样的多项式有个；若

，令，则是自然多项式，且，故，这样的多项式有个.

所以，.

式①成立.

其次证明：对任何正整数，有. ②

由式①可知，不减，且对，有

.

特别地，令，有.

故.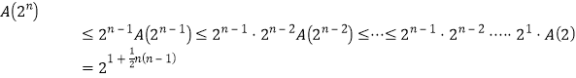

式②的右边获证.

取整数，使.

则.

取自然数组（），使，这样的数组（）有个.

对每个这样的数组，再取，其中，，令，则，且，有.

从而，是自然多项式.因此，.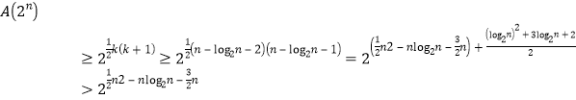

故式②的左边获证.

由式②有.

令，得.

对任意的正整数，设.则，.

又由不减可知，.

则.

令，，得.