
【题目】已知函数φ(x)= ![]() ,a>0
,a>0
(1)若函数f(x)=lnx+φ(x),在(1,2)上只有一个极值点,求a的取值范围;
(2)若g(x)=|lnx|+φ(x),且对任意x1 , x2∈(0,2],且x1≠x2 , 都有 ![]() <﹣1,求a的取值范围.
<﹣1,求a的取值范围.
【答案】
(1)解: f(x)=lnx+φ(x)=lnx+ ![]() ,(x>0,a>0),
,(x>0,a>0),
f′(x)= ![]() ﹣
﹣ ![]() ,
,
当f′(1)f′(2)<0时,函数f(x)在区间(1,2)上只有一个极值点,
即为(1﹣ ![]() a)(
a)( ![]() ﹣
﹣ ![]() a)<0,
a)<0,
解得:4<a< ![]() ;
;
(2)解:∵ ![]() <﹣1,
<﹣1,
∴有 ![]() +1<0,
+1<0,
∴ ![]() <0,
<0,
设h(x)=g(x)+x,依题意,h(x)在(0,2]上是减函数.
当1≤x≤2时,h(x)=lnx+ ![]() +x,h′(x)=
+x,h′(x)= ![]() ﹣
﹣ ![]() +1,
+1,
令h′(x)≤0,得:a≥ ![]() +(x+1)2=x2+3x+
+(x+1)2=x2+3x+ ![]() +3对x∈[1,2]恒成立,
+3对x∈[1,2]恒成立,
设m(x)=x2+3x+ ![]() +3,则m′(x)=2x+3﹣
+3,则m′(x)=2x+3﹣ ![]() ,
,
∵1≤x≤2,∴m′(x)=2x+3﹣ ![]() >0,
>0,
∴m(x)在[1,2]上递增,则当x=2时,m(x)有最大值为 ![]() ,
,
∴a≥ ![]() ;
;
当0<x<1时,h(x)=﹣lnx+ ![]() +x,h′(x)=﹣
+x,h′(x)=﹣ ![]() ﹣
﹣ ![]() +1,
+1,
令h′(x)≤0,得:a≥﹣ ![]() +(x+1)2=x2+x﹣
+(x+1)2=x2+x﹣ ![]() ﹣1,
﹣1,
设t(x)=x2+x﹣ ![]() ﹣1,则t′(x)=2x+1+
﹣1,则t′(x)=2x+1+ ![]() >0,
>0,
∴t(x)在(0,1)上是增函数,
∴t(x)<t(1)=0,
∴a≥0
【解析】(1)求出函数的导数,得到f′(1)f′(2)<0,解出即可;(2)设h(x)=g(x)+x,依题意得出h(x)在(0,2]上是减函数.下面对x分类讨论:①当1≤x≤2时,②当0<x<1时,利用导数研究函数的单调性从及最值,即可求得求a的取值范围.
【考点精析】本题主要考查了利用导数研究函数的单调性和函数的最大(小)值与导数的相关知识点,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值才能正确解答此题.
比较,其中最大的是一个最大值,最小的是最小值才能正确解答此题.


 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源: 题型:
【题目】为了了解当下高二男生的身高状况,某地区对高二年级男生的身高(单位: ![]() )进行了抽样调查,得到的频率分布直方图如图所示.已知身高在
)进行了抽样调查,得到的频率分布直方图如图所示.已知身高在![]() 之间的男生人数比身高在
之间的男生人数比身高在![]() 之间的人数少1人.
之间的人数少1人.

(1)若身高在![]() 以内的定义为身高正常,而该地区共有高二男生18000人,则该地区高二男生中身高正常的大约有多少人?
以内的定义为身高正常,而该地区共有高二男生18000人,则该地区高二男生中身高正常的大约有多少人?
(2)从所抽取的样本中身高在![]() 和
和![]() 的男生中随机再选出2人调查其平时体育锻炼习惯对身高的影响,则所选出的2人中至少有一人身高大于185
的男生中随机再选出2人调查其平时体育锻炼习惯对身高的影响,则所选出的2人中至少有一人身高大于185![]() 的概率是多少?
的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),在以原点为极点,
为参数),在以原点为极点, ![]() 轴正半轴为极轴的极坐标系中,直线
轴正半轴为极轴的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的倾斜角;
的倾斜角;
(2)设点![]() ,直线
,直线![]() 和曲线
和曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是两条不同的直线,
是两条不同的直线,![]() 是三个不同的平面,给出下列四个命题:①若
是三个不同的平面,给出下列四个命题:①若![]() ,则
,则![]() ; ②若
; ②若![]() 则
则![]() ;③若
;③若![]() ,则
,则![]() ; ④若
; ④若![]() ,则
,则![]() ,其中正确命题的序号是( )
,其中正确命题的序号是( )
A.①和②B.②和③C.③和④D.①和④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】微信红包是一款年轻人非常喜欢的手机应用.某网络运营商对甲、乙两个品牌各![]() 种型号的手机在相同环境下抢到红包的个数进行统计,得到如下数据:
种型号的手机在相同环境下抢到红包的个数进行统计,得到如下数据:
品牌 型号 | Ⅰ | Ⅱ | Ⅲ | Ⅳ | Ⅴ |
甲品牌(个) | 4 | 3 | 8 | 6 | 12 |
乙品牌(个) | 5 | 7 | 9 | 4 | 3 |
红包个数 手机品牌 | 优良 | 一般 | 合计 |
甲品牌(个) | |||
乙品牌(个) | |||
合计 |
(Ⅰ)如果抢到红包个数超过![]() 个的手机型号为“优良”,否则为“一般”,请完成上述表格,并据此判断是否有
个的手机型号为“优良”,否则为“一般”,请完成上述表格,并据此判断是否有![]() 的把握认为抢到红包的个数与手机品牌有关?
的把握认为抢到红包的个数与手机品牌有关?
(Ⅱ)不考虑其它因素,现要从甲、乙两品牌的![]() 种型号中各选出
种型号中各选出![]() 种型号的手机进行促销活动,求恰有一种型号是“优良”,另一种型号是“一般”的概率;
种型号的手机进行促销活动,求恰有一种型号是“优良”,另一种型号是“一般”的概率;
参考公式:随机变量![]() 的观察值计算公式:
的观察值计算公式:![]() ,
,
其中![]() .临界值表:
.临界值表:
| 0.10 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了实现绿色发展,避免浪费能源,某市政府计划对居民用电采用阶梯收费的方法.为此,相关部分在该市随机调查了![]() 户居民六月份的用电量(单位:
户居民六月份的用电量(单位:![]() )和家庭收入(单位:万元),以了解这个城市家庭用电量的情况.
)和家庭收入(单位:万元),以了解这个城市家庭用电量的情况.
用电量数据如下:
![]() .
.
对应的家庭收入数据如下:
![]()
![]() .
.
(Ⅰ)根据国家发改委的指示精神,该市计划实施![]() 阶阶梯电价,使
阶阶梯电价,使![]() 的用户在第一档,电价为
的用户在第一档,电价为![]() 元/
元/![]() ;
;![]() 的用户在第二档,电价为
的用户在第二档,电价为![]() 元/
元/![]() ;
;![]() 的用户在第三档,电价为
的用户在第三档,电价为![]() 元/
元/![]() ,试求出居民用电费用
,试求出居民用电费用![]() 与用电量
与用电量![]() 间的函数关系;
间的函数关系;
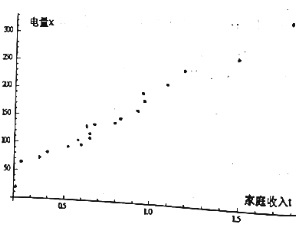
(Ⅱ)以家庭收入![]() 为横坐标,电量
为横坐标,电量![]() 为纵坐标作出散点图(如图),求
为纵坐标作出散点图(如图),求![]() 关于
关于![]() 的回归直线方程(回归直线方程的系数四舍五入保留整数).
的回归直线方程(回归直线方程的系数四舍五入保留整数).
(Ⅲ)小明家的月收入![]() 元,按上述关系,估计小明家月支出电费多少元?
元,按上述关系,估计小明家月支出电费多少元?
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
参考公式:一组相关数据![]() ,
,![]() ,…,
,…,![]() 的回归直线方程
的回归直线方程![]() 的斜率和截距的最小二乘法估计分别为
的斜率和截距的最小二乘法估计分别为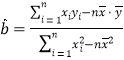 ,
,![]() ,其中
,其中![]() ,
,![]() 为样本均值.
为样本均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F为抛物线C:y2=4x的焦点,过F作两条互相垂直的直线l1 , l2 , 直线l1与C交于A、B两点,直线l2与C交于D、E两点,则|AB|+|DE|的最小值为( )
A.16
B.14
C.12
D.10
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着![]() 业的迅速发展计算机也在迅速更新换代,平板电脑因使用和移动便捷以及时尚新潮性,而备受人们尤其是大学生的青睐,为了解大学生购买平板电脑进行学习的学习情况,某大学内进行了一次匿名调查,共收到1500份有效问卷.调查结果显示700名女学生中有300人,800名男生中有400人拥有平板电脑.
业的迅速发展计算机也在迅速更新换代,平板电脑因使用和移动便捷以及时尚新潮性,而备受人们尤其是大学生的青睐,为了解大学生购买平板电脑进行学习的学习情况,某大学内进行了一次匿名调查,共收到1500份有效问卷.调查结果显示700名女学生中有300人,800名男生中有400人拥有平板电脑.
(Ⅰ)完成下列列联表:
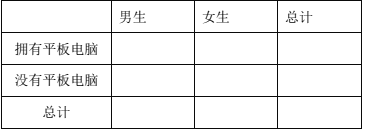
(Ⅱ)分析是否有![]() 的把握认为购买平板电脑与性别有关?
的把握认为购买平板电脑与性别有关?
附:独立性检验临界值表:

(参考公式:![]() ,其中
,其中![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com