
【题目】由于工作需要,某公司准备一次性购买两台具有智能打印、扫描、复印等多种功能的智能激光型打印机.针对购买后未来五年内的售后,厂家提供如下两种方案:
方案一:一次性缴纳![]() 元,在未来五年内,可免费上门维修
元,在未来五年内,可免费上门维修![]() 次,超过
次,超过![]() 次后每次收取费用
次后每次收取费用![]() 元;
元;
方案二:一次性缴纳![]() 元,在未来五年内,可免费上门维修
元,在未来五年内,可免费上门维修![]() 次,超过
次,超过![]() 次后每次收取费用
次后每次收取费用![]() 元.
元.
该公司搜集并整理了![]() 台这款打印机使用五年的维修次数,所得数据如下表所示:
台这款打印机使用五年的维修次数,所得数据如下表所示:
维修次数 |
|
|
|
|
台数 |
|
|
|
|
以这![]() 台打印机使用五年的维修次数的频率代替
台打印机使用五年的维修次数的频率代替![]() 台打印机使用五年的维修次数的概率,记
台打印机使用五年的维修次数的概率,记![]() 表示这两台智能打印机五年内共需维修的次数.
表示这两台智能打印机五年内共需维修的次数.
(1)求![]() 的分布列及数学期望;
的分布列及数学期望;
(2)以两种方案产生的维修费用的期望值为决策依据,写出你的选择,并说明理由.
 黄冈创优卷系列答案
黄冈创优卷系列答案科目:高中数学 来源: 题型:
【题目】在长方体ABCD-A1B1C1D1中(如图),AD=AA1=1,AB=2,点E是棱AB的中点.
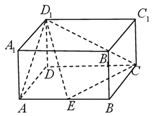
(1)求异面直线AD1与EC所成角的大小;
(2)《九章算术》中,将四个面都是直角三角形的四面体称为鳖臑,试问四面体D1CDE是否为鳖臑?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某制药厂准备投入适当的广告费,对产品进行宣传,在一年内,预计年销量Q(万件)与广告费x(万元)之间的函数关系为Q![]() (x≥0).已知生产此产品的年固定投入为3万元,每生产1万件此产品仍需后期再投入32万元,若每件售价为“年平均每件投入的150%”与“年平均每件所占广告费的50%”之和(注:投入包括“年固定投入”与“后期再投入”).
(x≥0).已知生产此产品的年固定投入为3万元,每生产1万件此产品仍需后期再投入32万元,若每件售价为“年平均每件投入的150%”与“年平均每件所占广告费的50%”之和(注:投入包括“年固定投入”与“后期再投入”).
(1)试将年利润w万元表示为年广告费x万元的函数,并判断当年广告费投入100万元时,企业亏损还是盈利?
(2)当年广告费投入多少万元时,企业年利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图(1),边长为![]() 的正方形
的正方形![]() 中,
中,![]() ,
,![]() 分别为
分别为![]() 、
、![]() 上的点,且
上的点,且![]() ,现沿
,现沿![]() 把
把![]() 剪切、拼接成如图(2)的图形,再将
剪切、拼接成如图(2)的图形,再将![]() ,
,![]() ,
,![]() 沿
沿![]() ,
,![]() ,
,![]() 折起,使
折起,使![]() 、
、![]() 、
、![]() 三点重合于点
三点重合于点![]() ,如图(3).
,如图(3).
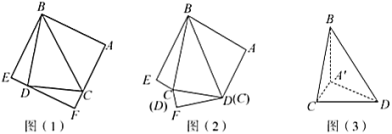
(1)求证:![]() ;
;
(2)求二面角![]() 最小时的余弦值.
最小时的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正方体![]() 的棱长为
的棱长为![]() ,点
,点![]() 为棱
为棱![]() 的中点.下列结论:①线段
的中点.下列结论:①线段![]() 上存在点
上存在点![]() ,使得
,使得![]() 平面
平面![]() ;②线段
;②线段![]() 上存在点
上存在点![]() ,使
,使![]() 得平面
得平面![]() ;③平面
;③平面![]() 把正方体分成两部分,较小部分的体积为
把正方体分成两部分,较小部分的体积为![]() ,其中所有正确的序号是( )
,其中所有正确的序号是( )
A.①B.③C.①③D.①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市在开展创建“全国文明城市”活动中,工作有序扎实,成效显著,尤其是城市环境卫生大为改观,深得市民好评.“创文”过程中,某网站推出了关于环境治理和保护问题情况的问卷调查,现从参与问卷调查的人群中随机选出200人,并将这200人按年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
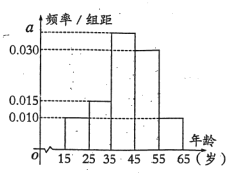
(1)求出a的值;
(2)若已从年龄较小的第1,2组中用分层抽样的方法抽取5人,现要再从这5人中随机抽取3人进行问卷调查,求第2组恰好抽到2人的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出如下四个命题:①若“![]() 且
且![]() ”为假命题,则
”为假命题,则![]() 均为假命题;②命题“若
均为假命题;②命题“若![]() ,则
,则![]() ”的否命题为“若
”的否命题为“若![]() ,则
,则![]() ”;③命题“
”;③命题“![]() ,
,![]() ”的否定是“
”的否定是“![]() ,
,![]() ”;④在
”;④在![]() 中,“
中,“![]() ”是“
”是“![]() ”的充要条件.其中正确的命题是( )
”的充要条件.其中正确的命题是( )
A.②③④B.①③④C.①②④D.①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年国庆黄金周影市火爆依旧,《我和我的祖国》、《中国机长》、《攀登者》票房不断刷新,为了解我校高三2300名学生的观影情况,随机调查了100名在校学生,其中看过《我和我的祖国》或《中国机长》的学生共有80位,看过《中国机长》的学生共有60位,看过《中国机长》且看过《我和我的祖国》的学生共有50位,则该校高三年级看过《我和我的祖国》的学生人数的估计值为( )
A.1150B.1380C.1610D.1860
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com