分析:抛物线y
2=4x焦点F(1,0)恰好是圆(x-1)
2+y
2=1的圆心是(1,0),若直线的斜率不存在,则直线方程为x=1,
代入抛物线方程和圆的方程,可直接得到ABCD四个点的坐标为(1,2)(1,1)(1,-1)(1,-2),由此能求出
•=1.若直线的斜率存在,设为k,则直线方程为y=k(x-1),设A(x
1,y
1),B(x
2,y
2),把直线方程与抛物线方程联立,得k
2x
2-(2k
2+4)x+k
2=0,由韦达定理有x
1x
2=1,由抛物线的焦点F同时是已知圆的圆心,知|
|=|
|-|
|=x
1,|
|=|
|-|
|=x
2,由此能求出
•=1.
解答:解:∵抛物线y
2=4x焦点F(1,0),p=2,
圆(x-1)
2+y
2=1的圆心是(1,0)半径r=1,
设A(x
1,y
1),D(x
2,y
2),
过抛物线y
2=4x的焦点F的直线依次交抛物线及圆(x-1)
2+y
2=1于点A,B,C,D,
A,D在圆上,B,C在抛物线上
1.若直线的斜率不存在,则直线方程为x=1,
代入抛物线方程和圆的方程,
可直接得到ABCD四个点的坐标为(1,2)(1,1)(1,-1)(1,-2),
所以
=(0,-1),=(0,-1),
•=1.
2.若直线的斜率存在,设为k,则直线方程为y=k(x-1),
因为直线过抛物线的焦点(1,0)
不妨设A(x
1,y
1),B(x
2,y
2),
过AB分别作抛物线准线的垂线,由抛物线的定义,|AF|=x
1+1,|DF|=x
2+1,
把直线方程与抛物线方程联立,消去y可得
k
2x
2-(2k
2+4)x+k
2=0,
由韦达定理有x
1x
2=1,
而抛物线的焦点F同时是已知圆的圆心,
所以|
|=|
|=r=1,
从而有|
|=|
|-|
|=x
1,
|
|=|
|-|
|=x
2,
∵A,B,C,D四点共线,
∴
•=|
|•
||=x
1x
2=1.
点评:本题主要考查抛物线标准方程,简单几何性质,直线与抛物线的位置关系,圆的简单性质等基础知识.考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.

 如图,过抛物线y2=4x焦点的直线依次交抛物线与圆(x-1)2+y2=1于A,B,C,D,则
如图,过抛物线y2=4x焦点的直线依次交抛物线与圆(x-1)2+y2=1于A,B,C,D,则

 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案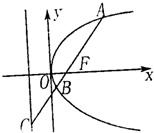 如图,过抛物线y2=2px(p>0)的焦点F的直线l交抛物线于点A、B,交其准线于点C,若|BC|=2|BF|,且|AF|=3,则此抛物线的方程为
如图,过抛物线y2=2px(p>0)的焦点F的直线l交抛物线于点A、B,交其准线于点C,若|BC|=2|BF|,且|AF|=3,则此抛物线的方程为 如图,过抛物线y2=2px(p>0)的焦点F的直线l交抛物线于点A、B(|AF|>|BF|),交其准线于点C,若|BC|=2|BF|,且|AF|=2,则此抛物线的方程为
如图,过抛物线y2=2px(p>0)的焦点F的直线l交抛物线于点A、B(|AF|>|BF|),交其准线于点C,若|BC|=2|BF|,且|AF|=2,则此抛物线的方程为