
【题目】已知曲线C的极坐标方程为ρ=2,在以极点为直角坐标原点O,极轴为x轴的正半轴建立的平面直角坐标系xOy中,直线l的参数方程为  (t为参数).
(t为参数).
(1)写出直线l的普通方程与曲线C的直角坐标方程;
(2)在平面直角坐标系中,设曲线C经过伸缩变换φ:  得到曲线C′,若M(x,y)为曲线C′上任意一点,求点M到直线l的最小距离.
得到曲线C′,若M(x,y)为曲线C′上任意一点,求点M到直线l的最小距离.
【答案】
(1)解:曲线C的极坐标方程为ρ=2,化为直角坐标方程:x2+y2=4.
直线l的参数方程为 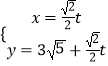 (t为参数),消去参数t化为普通方程:y=x+3
(t为参数),消去参数t化为普通方程:y=x+3 ![]()
(2)解:曲线C经过伸缩变换φ:  ,即
,即 ![]() ,代入曲线C的方程可得:4(x′)2+(y′)2=4,即得到曲线C′:
,代入曲线C的方程可得:4(x′)2+(y′)2=4,即得到曲线C′: ![]() =1.
=1.
若M(x,y)为曲线C′上任意一点,设M(cosθ,2sinθ),点M到直线l的距离d= ![]() =
= ![]() ≥
≥ ![]() =
= ![]() ,当且仅当sin(θ﹣φ)=1时取等号.
,当且仅当sin(θ﹣φ)=1时取等号.
因此最小距离为: ![]()
【解析】(1)曲线C的极坐标方程为ρ=2,利用互化公式化为直角坐标方程.直线l的参数方程为 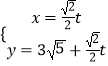 (t为参数),相减消去参数t化为普通方程.(2)曲线C经过伸缩变换φ:
(t为参数),相减消去参数t化为普通方程.(2)曲线C经过伸缩变换φ:  ,即
,即 ![]() ,代入曲线C的方程可得:4(x′)2+(y′)2=4,即得到曲线C′:
,代入曲线C的方程可得:4(x′)2+(y′)2=4,即得到曲线C′: ![]() =1.设M(cosθ,2sinθ),点M到直线l的距离d=
=1.设M(cosθ,2sinθ),点M到直线l的距离d= ![]() =
= ![]() ,即可得出最小值.
,即可得出最小值.


 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex﹣alnx﹣a. (Ⅰ)当a=e时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(Ⅱ)证明:对于a∈(0,e),f(x)在区间 ![]() 上有极小值,且极小值大于0.
上有极小值,且极小值大于0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2+(1﹣2a)x﹣lnx(a∈R).
(1)求函数f(x)在区间[1,2]上的最大值;
(2)若A(x1 , y1),B(x2 , y2),C(x0 , y0)是函数f(x)图象上不同的三点,且x0= ![]() ,试判断f′(x0)与
,试判断f′(x0)与 ![]() 之间的大小关系,并证明.
之间的大小关系,并证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知x,y∈R,m+n=7,f(x)=|x﹣1|﹣|x+1|.
(1)解不等式f(x)≥(m+n)x;
(2)设max{a,b}= ![]() ,求F=max{|x2﹣4y+m|,|y2﹣2x+n|}的最小值.
,求F=max{|x2﹣4y+m|,|y2﹣2x+n|}的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(sinx,mcosx),
=(sinx,mcosx), ![]() =(3,﹣1).
=(3,﹣1).
(1)若 ![]() ∥
∥ ![]() ,且m=1,求2sin2x﹣3cos2x的值;
,且m=1,求2sin2x﹣3cos2x的值;
(2)若函数f(x)= ![]()
![]() 的图象关于直线x=
的图象关于直线x= ![]() 对称,求函数f(2x)在[
对称,求函数f(2x)在[ ![]() ,
, ![]() ]上的值域.
]上的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题,松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等,如图是源于其思想的一个程序框图,若输入的a=10,b=4,则输出的n=( ) 
A.4
B.5
C.6
D.7
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且Sn+2=2an , 等差数列{bn}的前n项和为Tn , 且T2=S2=b3 .
(1)求数列{bn}的通项公式;
(2)令 ![]() ,求数列{cn}的前n项和Rn .
,求数列{cn}的前n项和Rn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设|θ|< ![]() ,n为正整数,数列{an}的通项公式an=sin
,n为正整数,数列{an}的通项公式an=sin ![]() tannθ,其前n项和为Sn
tannθ,其前n项和为Sn
(1)求证:当n为偶函数时,an=0;当n为奇函数时,an=(﹣1) ![]() tannθ;
tannθ;
(2)求证:对任何正整数n,S2n= ![]() sin2θ[1+(﹣1)n+1tan2nθ].
sin2θ[1+(﹣1)n+1tan2nθ].
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com