
ЁОЬтФПЁПжабыеўИЎЮЊСЫгІЖдвђШЫПкРЯСфЛЏЖјдьГЩЕФРЭЖЏСІЖЬШБЕШЮЪЬтЃЌФтЖЈГіЬЈЁАбгГйЭЫанФъСфеўВпЁБЃЌЮЊСЫСЫНтШЫУЧЖдЁАбгГйЭЫанФъСфеўВпЁБЕФЬЌЖШЃЌд№ГЩШЫЩчВПНјааЕїбаЃЌШЫЩчВПДгЭјЩЯФъСфдк15ЁЋ65ЫъЕФШЫШКжаЫцЛњЕїВщ100ШЫЃЌЕїВщЪ§ОнЕФЦЕТЪЗжВМжБЗНЭМКЭжЇГжЁАбгГйЭЫанЁБЕФШЫЪ§гыФъСфЕФЭГМЦНсЙћШчЯТЃК
ФъСф | [15ЃЌ25ЃЉ | [25ЃЌ35ЃЉ | [35ЃЌ45ЃЉ | [45ЃЌ55ЃЉ | [55ЃЌ65] |
жЇГжЁАбгГйЭЫанЁБЕФШЫЪ§ | 15 | 5 | 15 | 28 | 17 |
ЃЈ1ЃЉгЩвдЩЯЭГМЦЪ§ОнЬю2ЁС2СаСЊБэЃЌВЂХаЖЯЪЧЗё95%ЕФАбЮеШЯЮЊвд45ЫъЮЊНчЕуЕФВЛЭЌШЫШКЖдЁАбгГйЭЫанФъСфеўВпЁБЕФжЇГжгаВювьЃЛ
45ЫъвдЯТ | 45ЫъвдЩЯ | змМЦ | |
жЇГж | |||
ВЛжЇГж | |||
змМЦ |
ЃЈ2ЃЉШєвд45ЫъЮЊЗжНчЕуЃЌДгВЛжЇГжЁАбгГйЭЫанЁБЕФШЫжаАДЗжВуГщбљЕФЗНЗЈГщШЁ8ШЫВЮМгФГЯюЛюЖЏЃЌЯжДгет8ШЫжаЫцЛњГщ2ШЫЃЎ
ЂйГщЕН1ШЫЪЧ45ЫъвдЯТЪБЃЌЧѓГщЕНЕФСэвЛШЫЪЧ45ЫъвдЩЯЕФИХТЪЃЛ
ЂкМЧГщЕН45ЫъвдЩЯЕФШЫЪ§ЮЊXЃЌЧѓЫцЛњБфСПXЕФЗжВМСаМАЪ§бЇЦкЭћЃЎ
PЃЈK2Ёнk0ЃЉ | 0.100 | 0.050 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 6.635 | 10.828 |
![]() ЃЎ
ЃЎ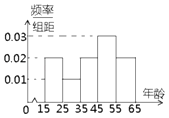
ЁОД№АИЁП
ЃЈ1ЃЉНтЃКгЩЭГМЦЪ§ОнЬю2ЁС2СаСЊБэШчЯТЃЌ
45ЫъвдЯТ | 45ЫъвдЩЯ | змМЦ | |
жЇГж | 35 | 45 | 80 |
ВЛжЇГж | 15 | 5 | 20 |
змМЦ | 50 | 50 | 100 |
МЦЫуЙлВтжЕ ![]() ЃЌ
ЃЌ
Ыљвдга95%ЕФАбЮеШЯЮЊвд45ЫъЮЊЗжНчЕуЕФВЛЭЌШЫШКЖдЁАбгГйЭЫанеўВпЁБЕФжЇГжЖШгаВювьЃЛ
ЃЈ2ЃЉЂйГщЕН1ШЫЪЧ45ЫъвдЯТЕФИХТЪ ![]() ЃЌГщЕН1ШЫЪЧ45ЫъвдЩЯЕФИХТЪЪЧ
ЃЌГщЕН1ШЫЪЧ45ЫъвдЩЯЕФИХТЪЪЧ ![]() ЃЌ
ЃЌ
ЙЪЫљЧѓЕФИХТЪЪЧP= ![]() ЁС
ЁС ![]() =
= ![]() ЃЛ
ЃЛ
ЂкИљОнЬтвтЃЌXЕФПЩФмШЁжЕЪЧ0ЃЌ1ЃЌ2ЃЛ
МЦЫуPЃЈX=0ЃЉ= ![]() =
= ![]() ЃЌ
ЃЌ
PЃЈX=1ЃЉ= ![]() =
= ![]() ЃЌ
ЃЌ
PЃЈX=2ЃЉ= ![]() =
= ![]() ЃЌ
ЃЌ
ПЩЕУЫцЛњБфСПXЕФЗжВМСаЮЊ
X | 0 | 1 | 2 |
P |
|
|
|
ЙЪЪ§бЇЦкЭћЮЊEЃЈXЃЉ=0ЁС ![]() +1ЁС
+1ЁС ![]() +2ЁС
+2ЁС ![]() =
= ![]() ЃЎ
ЃЎ
ЁОНтЮіЁПЃЈ1ЃЉгЩЭГМЦЪ§ОнЕУЕН2ЁС2СаСЊБэЃЌИљОнЙЋЪНПЩЕУЕНK 2=6.25 > 3.841ЃЌЙЪга95%ЕФАбЮеШЯЮЊвд45ЫъЮЊЗжНчЕуЕФВЛЭЌШЫШКЖдЁАбгГйЭЫанеўВпЁБЕФжЇГжЖШгаВювьЃЛЃЈ2ЃЉЗжБ№ЧѓГіГщЕН1ШЫЪЧ45ЫъвдЯТЕФИХТЪЃЌГщЕН1ШЫЪЧ45ЫъвдЩЯЕФИХТЪЃЌЙЪЫљЧѓЕФИХТЪЮЊ![]() ЃЌ ИљОнЬтвтЃЌXЕФПЩФмШЁжЕЪЧ0ЃЌ1ЃЌ2ЃЛЗжБ№ЫуГіИХТЪЃЌСаГіЗжВМСаЃЌЕУЕНЪ§бЇЦкЭћ.
ЃЌ ИљОнЬтвтЃЌXЕФПЩФмШЁжЕЪЧ0ЃЌ1ЃЌ2ЃЛЗжБ№ЫуГіИХТЪЃЌСаГіЗжВМСаЃЌЕУЕНЪ§бЇЦкЭћ.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§fЃЈxЃЉ=exЉaxЉ1ЃЈeЮЊздШЛЖдЪ§ЕФЕзЪ§ЃЉЃЎ
ЃЈЂёЃЉЧѓКЏЪ§fЃЈxЃЉЕФЕЅЕїЧјМфЃЛ
ЃЈЂђЃЉЕБaЃО0ЪБЃЌШєfЃЈxЃЉЁн0ЖдШЮвтЕФxЁЪRКуГЩСЂЃЌЧѓЪЕЪ§aЕФжЕЃЛ
ЃЈЂѓЃЉЧѓжЄЃК ![]() ЃЎ
ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНЋКЏЪ§fЃЈxЃЉ=sinЃЈ2xЉ ![]() ЃЉЕФЭМЯѓЯђгвЦНвЦ
ЃЉЕФЭМЯѓЯђгвЦНвЦ ![]() ИіЕЅЮЛКѓЕУЕНКЏЪ§gЃЈxЃЉЃЌдђgЃЈxЃЉОпгааджЪЃЈЁЁЁЁЃЉ
ИіЕЅЮЛКѓЕУЕНКЏЪ§gЃЈxЃЉЃЌдђgЃЈxЃЉОпгааджЪЃЈЁЁЁЁЃЉ
A.зюДѓжЕЮЊ1ЃЌЭМЯѓЙигкжБЯпx= ![]() ЖдГЦ
ЖдГЦ
B.дкЃЈ0ЃЌ ![]() ЃЉЩЯЕЅЕїЕнМѕЃЌЮЊЦцКЏЪ§
ЃЉЩЯЕЅЕїЕнМѕЃЌЮЊЦцКЏЪ§
C.дкЃЈЉ ![]() ЃЌ
ЃЌ ![]() ЃЉЩЯЕЅЕїЕндіЃЌЮЊХМКЏЪ§
ЃЉЩЯЕЅЕїЕндіЃЌЮЊХМКЏЪ§
D.жмЦкЮЊІаЃЌЭМЯѓЙигкЕуЃЈ ![]() ЃЌ0ЃЉЖдГЦ
ЃЌ0ЃЉЖдГЦ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПКЏЪ§fЃЈxЃЉ=|x+3|+|xЉ1|ЃЌЦфзюаЁжЕЮЊtЃЎ
ЃЈ1ЃЉЧѓtЕФжЕЃЛ
ЃЈ2ЃЉШєе§ЪЕЪ§aЃЌbТњзуa+b=4ЃЌЧѓжЄ ![]() ЃЎ
ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМЋзјБъЯЕЕФМЋЕуЮЊжБНЧзјБъЯЕЕФдЕуЃЌМЋжсЮЊxжсЕФе§АыжсЃЌСНзјБъЯЕжаЕФЕЅЮЛГЄЖШЯрЭЌЃЌвбжЊЧњЯпCЕФМЋзјБъЗНГЬЮЊІб=2ЃЈsinІШ+cosІШЃЉЃЎ
ЃЈЂёЃЉЧѓCЕФжБНЧзјБъЗНГЬЃЛ
ЃЈЂђЃЉжБЯп 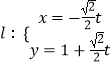 ЃЈtЮЊВЮЪ§ЃЉгыЧњЯпCНЛгкAЃЌBСНЕуЃЌгыyжсНЛгкEЃЌЧѓ|EA|+|EB|ЕФжЕЃЎ
ЃЈtЮЊВЮЪ§ЃЉгыЧњЯпCНЛгкAЃЌBСНЕуЃЌгыyжсНЛгкEЃЌЧѓ|EA|+|EB|ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮвЙњЙХДњЪ§бЇжјзїЁЖОХеТЫуЪѕЁЗгаШчЯТЮЪЬтЃКЁАНёгаЦїжаУзЃЌВЛжЊЦфЪ§ЃЌЧАШЫШЁАыЃЌжаШЫШ§ЗжШЁвЛЃЌКѓШЫЫФЗжШЁвЛЃЌгрУзвЛЖЗЮхЩ§ЃЎЮЪЃЌУзМИКЮЃПЁБШчЭМЪЧНтОіИУЮЪЬтЕФГЬађПђЭМЃЌжДааИУГЬађПђЭМЃЌШєЪфГіЕФS=1.5ЃЈЕЅЮЛЃКЩ§ЃЉЃЌдђЪфШыkЕФжЕЮЊЃЈЁЁЁЁЃЉ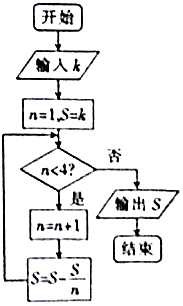
A.4.5
B.6
C.7.5
D.9
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЧњЯпCЕФВЮЪ§ЗНГЬЮЊ ![]() ЃЈІеЮЊВЮЪ§ЃЉЃЌвддЕуЮЊМЋЕуЃЌxжсЕФЗЧИКАыжсЮЊМЋжсНЈСЂМЋзјБъЯЕЃЎ
ЃЈІеЮЊВЮЪ§ЃЉЃЌвддЕуЮЊМЋЕуЃЌxжсЕФЗЧИКАыжсЮЊМЋжсНЈСЂМЋзјБъЯЕЃЎ
ЃЈЂёЃЉЧѓЧњЯпCЕФМЋзјБъЗНГЬЃЛ
ЃЈЂђЃЉвбжЊЧуаБНЧЮЊ135ЁуЧвЙ§ЕуPЃЈ1ЃЌ2ЃЉЕФжБЯпlгыЧњЯпCНЛгкMЃЌNСНЕуЃЌЧѓ ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊf'ЃЈxЃЉ=2x+mЃЌЧвfЃЈ0ЃЉ=0ЃЌКЏЪ§fЃЈxЃЉЕФЭМЯѓдкЕуAЃЈ1ЃЌfЃЈ1ЃЉЃЉДІЕФЧаЯпЕФаБТЪЮЊ3ЃЌЪ§Са ![]() ЕФЧАnЯюКЭЮЊSn ЃЌ дђS2017ЕФжЕЮЊЃЈЁЁЁЁЃЉ
ЕФЧАnЯюКЭЮЊSn ЃЌ дђS2017ЕФжЕЮЊЃЈЁЁЁЁЃЉ
A.![]()
B.![]()
C.![]()
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮвЙњЙХДњУћжјЁЖзЏзгЬьЯТЦЊЁЗжагавЛОфУћбдЁАвЛГпжЎщЂЃЌШеШЁЦфАыЃЌЭђЪРВЛНпЁБЃЌЦфвтЫМЮЊЃКвЛГпЕФФОЙїЃЌУПЬьНиШЁвЛАыЃЌгРдЖЖМНиВЛЭъЃЌЯжНЋИУФОЙївРДЫЙцТЩНиШЁЃЌШчЭМЫљЪОЕФГЬађПђЭМЕФЙІФмОЭЪЧМЦЫуНиШЁ7ЬьКѓЫљЪЃФОЙїЕФГЄЖШЃЈЕЅЮЛЃКГпЃЉЃЌдђЂйЂкЂлДІПЩЗжБ№ЬюШыЕФЪЧЃЈЁЁЁЁЃЉ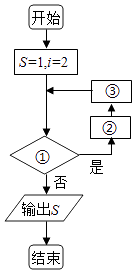
A.ЂйiЁм7ЃПЂкs=sЉ ![]() Ђлi=i+1
Ђлi=i+1
B.ЂйiЁм128ЃПЂкs=sЉ ![]() Ђлi=2i
Ђлi=2i
C.ЂйiЁм7ЃПЂкs=sЉ ![]() Ђлi=i+1
Ђлi=i+1
D.ЂйiЁм128ЃПЂкs=sЉ ![]() Ђлi=2i
Ђлi=2i
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com