
分析 设圆锥的底面半径为r,结合已知可得圆锥的表面积S=πr(r+$\sqrt{{r}^{2}+{48}^{2}}$)=4π×242,求出底面半径,代入圆锥体积公式,可得答案.
解答 解:∵球的半径为24cm,圆锥的高等于这个球的直径,
∴圆锥的高h=48cm,
设圆锥的底面半径为r,则圆锥的母线长为:$\sqrt{{r}^{2}+{48}^{2}}$cm,
故圆锥的表面积S=πr(r+$\sqrt{{r}^{2}+{48}^{2}}$)=4π×242cm2,
解得:r=16$\sqrt{3}$cm,
故圆锥的体积V=$\frac{1}{3}{πr}^{2}h$=12288πcm3,
故答案为:12288π
点评 本题考查的知识点是旋转体,圆锥的几何特征,球的表面积公式,难度中档.


科目:高中数学 来源: 题型:解答题
| 睡眠时间(小时) | [4,5) | [5,6) | [6,7) | [7,8) | [8,9) |
| 人数 | 1 | 5 | 6 | 5 | 3 |
| 睡眠时间(小时) | [4,5) | [5,6) | [6,7) | [7,8) | [8,9) |
| 人数 | 2 | 4 | 8 | 4 | 2 |
| 睡眠时间少于7小时 | 睡眠时间不少于7小时 | 合计 | |
| 男生 | |||
| 女生 | |||
| 合计 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
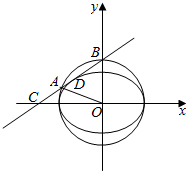 已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),点B为圆O:x2+y2=a2与y轴的交点,过点B的直线l(斜率为正)与椭圆相切于点D,并交x轴于点C,O为坐标原点,如图.
已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),点B为圆O:x2+y2=a2与y轴的交点,过点B的直线l(斜率为正)与椭圆相切于点D,并交x轴于点C,O为坐标原点,如图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 0 | C. | 2 | D. | 不存在 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com