练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】有甲、乙两个盒子，甲盒子里有个红球，乙盒子里有个红球和个黑球，现从乙盒子里随机取出个球放入甲盒子后，再从甲盒子里随机取一球，记取到的红球个数为个，则随着的增加，下列说法正确的是（ ）

    A.增加，增加B.增加，减小

    C.减小，增加D.减小，减小

    【答案】C

    【解析】

    由题意可知，从乙盒子里随机取出个球，含有红球个数服从超几何分布，即，可得出，再从甲盒子里随机取一球，则服从两点分布，所以，，从而可判断出和的增减性.

    由题意可知，从乙盒子里随机取出个球，含有红球个数服从超几何分布，即，其中，其中，且，.

    故从甲盒中取球，相当于从含有个红球的个球中取一球，取到红球个数为.

    故，

    随机变量服从两点分布，所以，随着的增大，减小；

    ，随着的增大，增大.

    故选：C.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （I）若曲线存在斜率为-1的切线，求实数a的取值范围；

    （II）求的单调区间；

    （III）设函数，求证：当时， 在上存在极小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，将斜边长为的等腰直角沿斜边上的高折成直二面角，为中点.

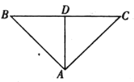
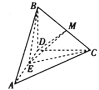
    （1）求二面角的余弦值；

    （2）为线段上一动点，当直线与平面所成的角最大时，求三棱锥外接球的体积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】鱼卷是泉州十大名小吃之一,不但本地人喜欢,而且深受外来游客的赞赏.小张从事鱼卷生产和批发多年,有着不少来自零售商和酒店的客户当地的习俗是农历正月不生产鱼卷,客户正月所需要的鱼卷都会在上一年农历十二月底进行一次性采购小张把去年年底采购鱼卷的数量x(单位:箱)在的客户称为“熟客”,并把他们去年采购的数量制成下表:

    采购数x

    客户数

    10

    10

    5

    20

    5

    (1)根据表中的数据作出频率分布直方图,并估计采购数在168箱以上(含168箱)的“熟客”人数;

    (2)若去年年底“熟客”们采购的鱼卷数量占小张去年年底总的销售量的,估算小张去年年底总的销售量(同一组中的数据用该组区间的中点值为代表);

    (3)由于鱼卷受到游客们的青睐,小张做了一份市场调查,决定今年年底是否在网上出售鱼卷,若不在网上出售鱼卷,则按去年的价格出售,每箱利润为20元,预计销售量与去年持平;若在网上出售鱼卷,则需把每箱售价下调2至5元,且每下调m元()销售量可增加1000m箱,求小张今年年底收入Y(单位:元)的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）求的单调区间；

    （2）当时，，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示的几何体中，四边形是菱形，是矩形，平面，，，，为的中点．

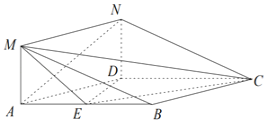
    （Ⅰ）求证：平面；

    （Ⅱ）求直线与平面所成角的正弦值；

    （Ⅲ）设为线段上的动点，二面角的平面角的大小为30°，求线段的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】“搜索指数”是网民通过搜索引擎，以每天搜索关键词的次数为基础所得到的统计指标.“搜索指数”越大，表示网民对该关键词的搜索次数越多，对该关键词相关的信息关注度也越高.下图是2017年9月到2018年2月这半年中，某个关键词的搜索指数变化的走势图.

    根据该走势图，下列结论正确的是（ ）

    A. 这半年中，网民对该关键词相关的信息关注度呈周期性变化

    B. 这半年中，网民对该关键词相关的信息关注度不断减弱

    C. 从网民对该关键词的搜索指数来看，去年10月份的方差小于11月份的方差

    D. 从网民对该关键词的搜索指数来看，去年12月份的平均值大于今年1月份的平均值

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，直线l的参数方程为（其中t为参数，）.在以原点O为极点，x轴的非负半轴为极轴所建立的极坐标系中，曲线C的极坐标方程为.设直线l与曲线C相交于A，B两点.

    （1）求曲线C和直线l的直角坐标方程；

    （2）已知点，求的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】皮埃尔·德·费马，法国律师和业余数学家，被誉为“业余数学家之王”，对数学界做出了重大贡献，其中在1636年发现了：若是质数，且互质，那么的次方除以的余数恒等于1，后来人们称该定理为费马小定理.依此定理若在数集中任取两个数，其中一个作为，另一个作为，则所取两个数不符合费马小定理的概率为（ ）

    A.B.C.D.

    查看答案和解析>>

    同步练习册答案