练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】直线ax＋by＝1与圆x2＋y2＝1相交于A，B两点(其中a，b是实数)，且△AOB是直角三角形(O是坐标原点)，则点P(a，b)与点(0,1)之间距离的最小值为________．

    【答案】－1

    【解析】根据题意画出图形，如图所示，

    过点O作OC⊥AB于C，因为△AOB为等腰直角三角形，所以C为弦AB的中点，又|OA|＝|OB|＝1，根据勾股定理得|AB|＝，∴|OC|＝|AB|＝.

    ∴圆心到直线的距离为＝，即2a2＋b2＝2，即a2＝－b2＋1≥0.

    ∴－≤b≤.则点P(a，b)与点(0,1)之间距离d＝＝＝.

    设f(b)＝b2－2b＋2＝(b－2)2，此函数为对称轴为x＝2的开口向上的抛物线，∴当－≤b≤<2时，函数为减函数．

    ∵f()＝3－2，∴d的最小值为＝＝－1

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，在长方形ABCD中，AB＝2，BC＝1，E为DC的中点，F为线段EC上一动点．现将△AFD沿AF折起，使平面ABD⊥平面ABC.在平面ABD内过点D作DK⊥AB，K为垂足．设AK＝t，则t的取值范围是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，．

    （1）若关于的方程只有一个实数解，求实数的取值范围；

    （2）若当时，不等式恒成立，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四棱锥PABC中，PA⊥底面ABCD，AD∥BC，AB=AD=AC=3，PA=BC=4，M为线段AD上一点，AM=2MD，N为PC的中点.

    （Ⅰ）证明MN∥平面PAB;

    （Ⅱ）求直线AN与平面PMN所成角的正弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f (x)＝x2－aln x－1，函数F(x)＝.

    (1)如果函数f (x)的图象上的每一点处的切线斜率都是正数，求实数a的取值范围；

    (2)当a＝2时，你认为函数y＝的图象与y＝F(x)的图象有多少个公共点？请证明你的结论.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某厂生产一种机器的固定成本为0.5万元，但每生产100台，需要加可变成本（即另增加投入）0.25万元，市场对此产品的年求量为500台，销售的收入函数为（万元）（），其中是产品售出的数量（单位：百台）.

    （1）把利润表示为年产量的函数；

    （2）年产量是多少时，工厂所得利润最大？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示,ABCD是边长为60 cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得ABCD四个点重合于图中的点P, 正好形成一个正四棱柱形状的包装盒,若要包装盒容积V(cm3)最大, 则EF长为____ cm ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，四棱锥的底面为矩形，已知， ，过底面对角线作与平行的平面交于.

    （1）试判定点的位置，并加以证明；

    （2）求二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在如图所示的多面体中，平面，平面，，且，是的中点.

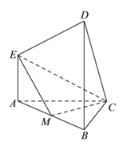
    （1）求证：；

    （2）求平面与平面所成的二面角的正弦值；

    （3）在棱上是否存在一点，使得直线与平面所成的角是. 若存在，指出点的位置；若不存在，请说明理由.

    查看答案和解析>>

    同步练习册答案