
【题目】函数![]() .
.
(Ⅰ)讨论![]() 的单调性;
的单调性;
(Ⅱ)当![]() 时,若
时,若![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)见解析(Ⅱ)![]()
【解析】试题分析:(1)求出导函数![]() 对
对![]() 分四种情况讨论:
分四种情况讨论: ![]() ,分别令
,分别令![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 增区间,
增区间, ![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 的减区间;(2)对
的减区间;(2)对![]() 讨论两种情况:
讨论两种情况: ![]() 时,由(1)知,
时,由(1)知, ![]() 在
在![]() 上单调递增,当
上单调递增,当![]() 时,
时, ![]() ,可得
,可得![]() ,符合题意;
,符合题意; ![]() 时,
时, ![]() 在
在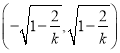 上单调递减,当
上单调递减,当![]() 时,
时, ![]() ,可证明
,可证明![]() ,不合题意,从而可得实数
,不合题意,从而可得实数![]() 的取值范围是
的取值范围是![]() .
.
试题解析:(1)由![]() 得
得![]() ,故
,故![]() 的定义域为
的定义域为![]() ,
, ![]() ,
,
因为![]() ,所以
,所以![]() ,
,
![]()
①当![]() 时,
时, ![]() 对
对![]() 恒成立,
恒成立,
![]() 在
在![]() 内无解,故
内无解,故![]() 在
在![]() 上单调递增;
上单调递增;
②当![]() 时,因为
时,因为![]() 恒成立,所以
恒成立,所以![]() 上
上![]() 单调递增;
单调递增;
③当![]() 时,
时, ![]() 恒成立,
恒成立, ![]() ,在
,在![]() 上
上![]() 单调递增;
单调递增;
④当![]() 时,由
时,由![]() ,得
,得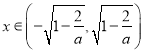 ,
,
由![]() ,得
,得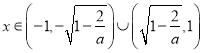 ,
,
故![]() 在
在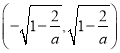 上单调递减,在
上单调递减,在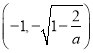 和
和 上单调递增,
上单调递增,
综上,当![]() 时,
时, ![]() 在
在![]() 上单调递增,
上单调递增,
当![]() 时,
时, ![]() 在
在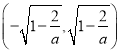 上单调递减,
上单调递减, ![]() 在
在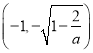 和
和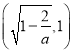 上单调递增.
上单调递增.
(2)①当![]() 时,由(1)知,
时,由(1)知, ![]() 在
在![]() 上单调递增,
上单调递增,
所以当![]() 时,
时, ![]() ,即
,即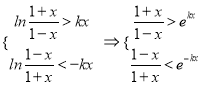 ,
,
两式相减得![]() ,
,
②当![]() 时,
时, ![]() 在
在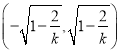 上单调递减,
上单调递减,
所以当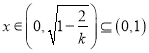 时,
时, ![]() ,
,
即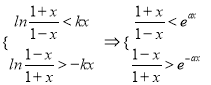 ,两式相减得
,两式相减得![]() ,
,
综上可知,当![]() 时,若
时,若![]() ,则实数
,则实数![]() 的取值范围是
的取值范围是![]()
【方法点晴】本题主要考查的是利用导数研究函数的单调性、不等式的恒成立和分类讨论思想的应用,属于难题.利用导数研究函数![]() 的单调性进一步求函数最值的步骤:①确定函数
的单调性进一步求函数最值的步骤:①确定函数![]() 的定义域;②对
的定义域;②对![]() 求导;③令
求导;③令![]() ,解不等式得
,解不等式得![]() 的范围就是递增区间;令
的范围就是递增区间;令![]() ,解不等式得
,解不等式得![]() 的范围就是递减区间;④根据单调性求函数
的范围就是递减区间;④根据单调性求函数![]() 的极值及最值(闭区间上还要注意比较端点处函数值的大小).
的极值及最值(闭区间上还要注意比较端点处函数值的大小).


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为F1(-c,0),F2(c,0),直线
的左、右焦点分别为F1(-c,0),F2(c,0),直线![]() 交椭圆E于A,B两点,△ABF1的周长为16,△AF1F2的周长为12.
交椭圆E于A,B两点,△ABF1的周长为16,△AF1F2的周长为12.
(1)求椭圆E的标准方程与离心率;
(2)若直线l与椭圆E交于C,D两点,且P(2,2)是线段CD的中点,求直线l的一般方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的首项a1=1,公差d>0.且a2,a5,a14分别是等比数列{bn}的b2,b3,b4.
(1)求数列{an}与{bn}的通项公式;
(2)设数列{cn}对任意自然数n均有![]() 成立,求c1+c2+…+c2016的值.
成立,求c1+c2+…+c2016的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义在R上的偶函数,f(x+1)为奇函数,f(0)=0,当x∈(0,1]时,f(x)=log2x,则在区间(8,9)内满足方程f(x)+2=![]() 的实数x为( )
的实数x为( )
A. ![]()
B. ![]()
C. ![]()
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列{an}中,a1=1,a2=2,数列{anan+1}是公比为q (q>0)的等比数列,则数列{an}的前2n项和S2n=____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD中,AP⊥平面PCD,AD∥BC,AB=BC=![]() AD,E,F分别为线段AD,PC的中点.
AD,E,F分别为线段AD,PC的中点.
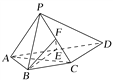
(1)求证:AP∥平面BEF;
(2)求证:BE⊥平面PAC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某P2P平台需要了解该平台投资者的大致年龄分布,发现其投资者年龄大多集中在区间[20,50]岁之间,对区间[20,50]岁的人群随机抽取20人进行了一次理财习惯调查,得到如下统计表和各年龄段人数频率分布直方图:
组数 | 分组 | 人数(单位:人) |
第一组 | [20,25) | 2 |
第二组 | [25,30) | a |
第三组 | [30,35) | 5 |
第四组 | [35,40) | 4 |
第五组 | [40,45) | 3 |
第六组 | [45,50] | 2 |

(Ⅰ)求a的值并画出频率分布直方图;
(Ⅱ)在统计表的第五与第六组的5人中,随机选取2人,求这2人的年龄都小于45岁的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直三棱柱ABC-A1B1C1中,AB=1,AC=2,BC=![]() ,D,E分别是AC1,BB1的中点,则直线DE与平面BB1C1C所成角的正弦值为________.
,D,E分别是AC1,BB1的中点,则直线DE与平面BB1C1C所成角的正弦值为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com