
【题目】在一次马拉松比赛中,30名运动员的成绩(单位:分钟)的茎叶图如图所示.若将运动员按成绩由好到差编号为1﹣30号,再用系统抽样方法从中抽取6人,则其中成绩在区间[130,151]上的运动员人数是( ) 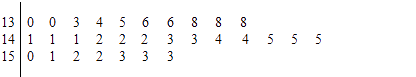
A.3
B.4
C.5
D.6
【答案】C
【解析】解:将运动员按成绩由好到差分成6组,则 第1组为(130,130,133,134,135),第2组为(136,136,138,138,138),
第3组为(141,141,141,142,142),第4组为(142,143,143,144,144),
第5组为(145,145,145,150,151),第6组为(152,152,153,153,153),
故成绩在区间[130,151]内的恰有5组,故有5人.
故选:C.
【考点精析】解答此题的关键在于理解茎叶图的相关知识,掌握茎叶图又称“枝叶图”,它的思路是将数组中的数按位数进行比较,将数的大小基本不变或变化不大的位作为一个主干(茎),将变化大的位的数作为分枝(叶),列在主干的后面,这样就可以清楚地看到每个主干后面的几个数,每个数具体是多少.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:高中数学 来源: 题型:
【题目】已知命题p:方程 ![]() +
+ ![]() =1表示焦点在y轴上的椭圆,命题q:双曲线
=1表示焦点在y轴上的椭圆,命题q:双曲线 ![]() ﹣
﹣ ![]() =1的离心率e∈(
=1的离心率e∈( ![]() ,
, ![]() ),若命题p、q中有且只有一个为真命题,则实数m的取值范围是
),若命题p、q中有且只有一个为真命题,则实数m的取值范围是
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在长方体ABCD﹣A1B1C1D1中,E,M,N分别是BC,AE,D1C的中点,AD=AA1 , AB=2AD. (Ⅰ)证明:MN∥平面ADD1A1;
(Ⅱ)求直线AD与平面DMN所成角θ的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在锐角△ABC中,a、b、c分别为角A、B、C所对的边,且 ![]() a=2csinA
a=2csinA
(1)确定角C的大小;
(2)若c= ![]() ,且△ABC的面积为
,且△ABC的面积为 ![]() ,求a+b的值.
,求a+b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,为迎接校庆,我校准备在直角三角形ABC内的空地上植造一块“绿地△ABD”,规划在△ABD的内接正方形BEFG内种花,其余地方种草,若AB=a,∠DAB=θ,种草的面积为S1 , 种花的面积为S2 , 比值 ![]() 称为“规划和谐度”.
称为“规划和谐度”.
(1)试用a,θ表示S1 , S2;
(2)若a为定值,BC足够长,当θ为何值时,“规划和谐度”有最小值,最小值是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆具有性质:若M,N是椭圆C: ![]() =1(a>b>0且a,b为常数)上关于y轴对称的两点,P是椭圆上的左顶点,且直线PM,PN的斜率都存在(记为kPM , kPN),则kPMkPN=
=1(a>b>0且a,b为常数)上关于y轴对称的两点,P是椭圆上的左顶点,且直线PM,PN的斜率都存在(记为kPM , kPN),则kPMkPN= ![]() .类比上述性质,可以得到双曲线的一个性质,并根据这个性质得:若M,N是双曲线C:
.类比上述性质,可以得到双曲线的一个性质,并根据这个性质得:若M,N是双曲线C: ![]() =1(a>0,b>0)上关于y轴对称的两点,P是双曲线C的左顶点,直线PM,PN的斜率都存在(记为kPM , kPN),双曲线的离心率e=
=1(a>0,b>0)上关于y轴对称的两点,P是双曲线C的左顶点,直线PM,PN的斜率都存在(记为kPM , kPN),双曲线的离心率e= ![]() ,则kPMkPN等于 .
,则kPMkPN等于 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在等腰直角△ABO中,设 ![]() =
= ![]() ,
, ![]() =
= ![]() ,|
,| ![]() |=|
|=| ![]() |=1,C为AB上靠近A点的三等分点,过C作AB的垂线l,设P为垂线上任一点,
|=1,C为AB上靠近A点的三等分点,过C作AB的垂线l,设P为垂线上任一点, ![]() =
= ![]() ,则
,则 ![]() (
( ![]() ﹣
﹣ ![]() )=( )
)=( ) 
A.![]()
B.﹣ ![]()
C.﹣ ![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}为等差数列,a1=2,{an}的前n项和为Sn , 数列{bn}为等比数列,且a1b1+a2b2+a3b3+…+anbn=(n﹣1)2n+2+4对任意的n∈N*恒成立.
(1)求数列{an}、{bn}的通项公式;
(2)是否存在非零整数λ,使不等式sin ![]() <
< ![]() 对一切n∈N*都成立?若存在,求出λ的值;若不存在,说明理由.
对一切n∈N*都成立?若存在,求出λ的值;若不存在,说明理由.
(3)各项均为正整数的无穷等差数列{cn},满足c39=a1007 , 且存在正整数k,使c1 , c39 , ck成等比数列,若数列{cn}的公差为d,求d的所有可能取值之和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于平面向量 ![]() ,
, ![]() ,
, ![]() ,下列结论正确的个数为( ) ①若
,下列结论正确的个数为( ) ①若 ![]()
![]() =
= ![]()
![]() ,则
,则 ![]() =
= ![]() ;
;
②若 ![]() =(1,k),
=(1,k), ![]() =(﹣2,6),
=(﹣2,6), ![]() ∥
∥ ![]() ,则k=﹣3;
,则k=﹣3;
③非零向量 ![]() 和
和 ![]() 满足|
满足| ![]() |=|
|=| ![]() |=|
|=| ![]() ﹣
﹣ ![]() |,则
|,则 ![]() 与
与 ![]() +
+ ![]() 的夹角为30°;
的夹角为30°;
④已知向量 ![]() ,且
,且 ![]() 与
与 ![]() 的夹角为锐角,则实数λ的取值范围是
的夹角为锐角,则实数λ的取值范围是 ![]() .
.
A.4个
B.3个
C.2个
D.1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com