
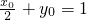 ,l1∩l2=M.
,l1∩l2=M.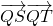 ≤4,求m的取值范围.
≤4,求m的取值范围.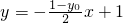 ,
,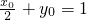 ,∴l1的方程是
,∴l1的方程是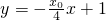
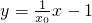 ,与l1的方程联立消去x0得
,与l1的方程联立消去x0得 ,
, (y≠-1)…(5分)
(y≠-1)…(5分)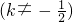
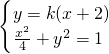 ,由方程消去y并整理得(1+4k2)x2+16k2x+16k2-4=0
,由方程消去y并整理得(1+4k2)x2+16k2x+16k2-4=0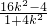 得x1=
得x1=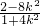 ,从而y1=
,从而y1=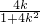
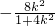 ,
, )…(7分)
)…(7分)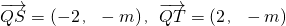 ,由
,由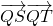 ≤4得:-2
≤4得:-2 ≤m≤2
≤m≤2 .
. =-
=- (x+
(x+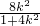 )
)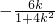
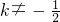 ,∴
,∴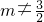 ,
,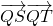 =-2x1-m(y1-m)=
=-2x1-m(y1-m)=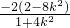 +
+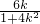 (
(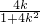 +
+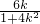 )=
)=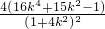 ≤4
≤4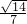 ≤k≤
≤k≤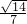 且k≠0,∴m=
且k≠0,∴m=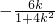 =
=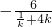
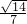 ≤k<0时,
≤k<0时,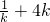 ≤-4;当0<k≤
≤-4;当0<k≤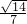 时,
时,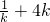 ≥4
≥4 ≤m≤
≤m≤ ,且m≠0
,且m≠0 ≤m<
≤m< ,且m≠0.…(12分)
,且m≠0.…(12分)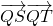 ≤4,即可得到结论.
≤4,即可得到结论.

 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| OA |
| OB |
| 12 |
| 5 |
| OP |
| OA |
| OB |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| 4 |
| 3 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 椭圆E:
椭圆E:| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 6 |
| ||
| 2 |
| 1 |
| 2 |
| AB |
| AN |
| BD |
| BN |
| 5 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2011-2012学年安徽省皖南八校高三第一次联考理科数学试卷 题型:解答题
(本小题满分12分)已知椭圆 过点A(a,0),B(0,b)的直
过点A(a,0),B(0,b)的直
线倾斜角为 ,原点到该直线的距离为
,原点到该直线的距离为 .
.
(1)求椭圆的方程;
(2)斜率小于零的直线过点D(1,0)与椭圆交于M,N两点,若 求直线MN的方程;
求直线MN的方程;
(3)是否存在实数k,使直线 交椭圆于P、Q两点,以PQ为直径的圆过点D(1,0)?若存在,求出k的值;若不存在,请说明理由。
交椭圆于P、Q两点,以PQ为直径的圆过点D(1,0)?若存在,求出k的值;若不存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com