
【题目】某大学高等数学这学期分别用![]() 两种不同的数学方式试验甲、乙两个大一新班(人数均为60人,入学数学平均分和优秀率都相同;勤奋程度和自觉性都一样).现随机抽取甲、乙两班各20名的高等数学期末考试成绩,得到茎叶图。 学校规定:成绩不得低于85分的为优秀
两种不同的数学方式试验甲、乙两个大一新班(人数均为60人,入学数学平均分和优秀率都相同;勤奋程度和自觉性都一样).现随机抽取甲、乙两班各20名的高等数学期末考试成绩,得到茎叶图。 学校规定:成绩不得低于85分的为优秀

(1)根据以上数据填写下列的![]() 的列联表
的列联表
甲 | 乙 | 总计 | |
成绩优秀 | |||
成绩不优秀 | |||
总计 |
(2)是否有![]() 的把握认为成绩优异与教学方式有关?”(计算保留三位有效数字)
的把握认为成绩优异与教学方式有关?”(计算保留三位有效数字)
下面临界值表仅供参考:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
科目:高中数学 来源: 题型:
【题目】为缓减人口老年化带来的问题,中国政府在2016年1月1日作出全国统一实施全面的“二孩”政策,生“二孩”是目前中国比较流行的元素![]() 某调查机构对某校学生做了一个是否同意父母生“二孩”抽样调查,该调查机构从该校随机抽查了100名不同性别的学生,调查统计他们是同意父母生“二孩”还是反对父母生“二孩”
某调查机构对某校学生做了一个是否同意父母生“二孩”抽样调查,该调查机构从该校随机抽查了100名不同性别的学生,调查统计他们是同意父母生“二孩”还是反对父母生“二孩”![]() 现已得知100人中同意父母生“二孩”占
现已得知100人中同意父母生“二孩”占![]() ,统计情况如表:
,统计情况如表:
性别属性 | 同意父母生“二孩” | 反对父母生“二孩” | 合计 |
男生 | 10 | ||
女生 | 30 | ||
合计 | 100 |
![]() 请补充完整上述列联表;
请补充完整上述列联表;
![]() 根据以上资料你是否有
根据以上资料你是否有![]() 把握,认为是否同意父母生“二孩”与性别有关?请说明理由.
把握,认为是否同意父母生“二孩”与性别有关?请说明理由.
参考公式与数据:![]() ,其中
,其中![]()
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 对任意的
对任意的![]() 均有
均有![]() 则称函数
则称函数![]() 具有性质
具有性质![]()
(Ⅰ)判断下面两个函数是否具有性质![]() 并说明理由.
并说明理由.
①![]() ②
②![]()
(Ⅱ)若函数![]() 具有性质
具有性质![]() ,且
,且![]()
求证:对任意![]() 有
有![]()
(Ⅲ)在(Ⅱ)的条件下,是否对任意![]() 均有
均有![]() 若成立,给出证明;若不成立,给出反例.
若成立,给出证明;若不成立,给出反例.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着智能手机和电子阅读器越来越普及,人们的阅读习惯也发生了改变,手机和电子阅读产品方便易携带,越来越多的人习惯通过手机或电子阅读器阅读.某电子书阅读器厂商随机调查了![]() 人,统计了这
人,统计了这![]() 人每日平均通过手机或电子阅读器阅读的时间(单位:分钟),由统计数据得到如下频率分布直方图,已知阅读时间在
人每日平均通过手机或电子阅读器阅读的时间(单位:分钟),由统计数据得到如下频率分布直方图,已知阅读时间在![]() ,
, ![]() ,
, ![]() 三组对应的人数依次成等差数列.
三组对应的人数依次成等差数列.
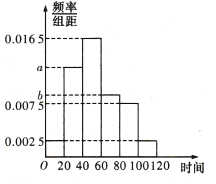
(1)求频率分布直方图中![]() ,
, ![]() 的值;
的值;
(2)若将日平均阅读时间不少于![]() 分钟的用户定义为“电子阅读发烧友”,将日平均阅读时间少于
分钟的用户定义为“电子阅读发烧友”,将日平均阅读时间少于![]() 分钟的用户定义为“电子阅读潜在爱好者”,现从上述“电子阅读发烧友”与“电子阅读潜在爱好者”的人中按分层抽样选出
分钟的用户定义为“电子阅读潜在爱好者”,现从上述“电子阅读发烧友”与“电子阅读潜在爱好者”的人中按分层抽样选出![]() 人,再从这
人,再从这![]() 人中任取
人中任取![]() 人,求恰有
人,求恰有![]() 人为“电子阅读发烧友”的概率.
人为“电子阅读发烧友”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人参加某种选拔测试.规定每人必须从备选的6道题中随机抽出3道题进行测试,在备选的6道题中,甲答对其中每道题的概率都是![]() ,乙只能答对其中的3道题.答对一题加10分,答错一题(不答视为答错)得0分.
,乙只能答对其中的3道题.答对一题加10分,答错一题(不答视为答错)得0分.
(1)求乙得分的分布列和数学期望;
(2)规定:每个人至少得20分才能通过测试,求甲、乙两人中至少有一人通过测试的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C的中心在原点,焦点在x轴上,离心率等于![]() ,它的一个顶点恰好是抛物线
,它的一个顶点恰好是抛物线![]() 的焦点.
的焦点.
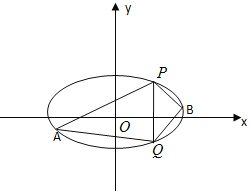
(Ⅰ)求椭圆C的方程;
(Ⅱ)点P(2,3), Q(2,-3)在椭圆上,A,B是椭圆上位于直线PQ两恻的动点,
①若直线AB的斜率为![]() ,求四边形APBQ面积的最大值;
,求四边形APBQ面积的最大值;
②当A、B运动时,满足于∠APQ=∠BPQ,试问直线AB的斜率是否为定值,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校艺术节对同一类的![]() ,
,![]() ,
,![]() ,
,![]() 四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
甲说:“是![]() 或
或![]() 作品获得一等奖”;
作品获得一等奖”;
乙说:“![]() 作品获得一等奖”;
作品获得一等奖”;
丙说:“![]() ,
,![]() 两项作品未获得一等奖”;
两项作品未获得一等奖”;
丁说:“是![]() 作品获得一等奖”.
作品获得一等奖”.
若这四位同学中只有两位说的话是对的,则获得一等奖的作品是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列有关命题的说法中错误的是( )
A. 设![]() ,则“
,则“![]() ”是“
”是“![]() ”的充要条件
”的充要条件
B. 若![]() 为真命题,则
为真命题,则![]() ,
, ![]() 中至少有一个为真命题
中至少有一个为真命题
C. 命题:“若![]() 是幂函数,则
是幂函数,则![]() 的图象不经过第四象限”的否命题是假命题
的图象不经过第四象限”的否命题是假命题
D. 命题“![]() ,
, ![]() 且
且![]() ”的否定形式是“
”的否定形式是“![]() ,
, ![]() 且
且![]() ”
”
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com