
已知抛物线 的焦点
的焦点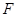 以及椭圆
以及椭圆 的上、下焦点及左、右顶点均在圆
的上、下焦点及左、右顶点均在圆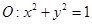 上.
上.
(1)求抛物线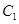 和椭圆
和椭圆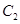 的标准方程;
的标准方程;
(2)过点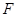 的直线交抛物线
的直线交抛物线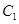 于
于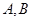 两不同点,交
两不同点,交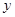 轴于点
轴于点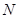 ,已知
,已知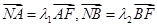 ,求
,求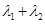 的值;
的值;
(3)直线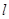 交椭圆
交椭圆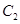 于
于 两不同点,
两不同点, 在
在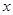 轴的射影分别为
轴的射影分别为 ,
, ,若点
,若点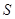 满足
满足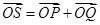 ,证明:点
,证明:点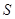 在椭圆
在椭圆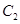 上.
上.
(1)  ,
, ;(2)-1;(3)详见解析.
;(2)-1;(3)详见解析.
【解析】
试题分析:(1)根据抛物线的焦点坐标满足圆的方程确定等量关系,求解抛物线方程;根据椭圆的焦点和右定点也在圆上,确定椭圆方程;(2)利用已知的向量关系式进行坐标转化求出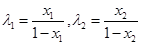 ,然后通过直线与抛物线方程联立,借助韦达定理进行化简
,然后通过直线与抛物线方程联立,借助韦达定理进行化简 并求值;(3)借助向量问题坐标化和点在椭圆上,明确点S的坐标,进而证明其在椭圆
并求值;(3)借助向量问题坐标化和点在椭圆上,明确点S的坐标,进而证明其在椭圆 上.
上.
试题解析:(1)由抛物线 的焦点
的焦点 在圆
在圆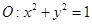 上得:
上得: ,
,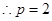
∴抛物线 .
2分
.
2分
同理由椭圆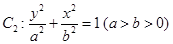 的上、下焦点
的上、下焦点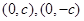 及左、右顶点
及左、右顶点 均在
均在
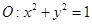 上可解得:
上可解得: .
.
得椭圆 .
4分
.
4分
(2)设直线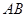 的方程为
的方程为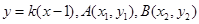 ,则
,则 .
.
联立方程组 ,消去
,消去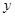 得:
得:
 且
且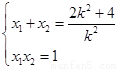 5分
5分
由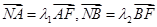 得:
得:
整理得: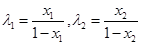
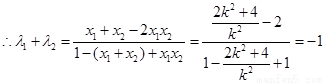 .
8分
.
8分
(3)设 ,则
,则
由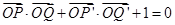 得
得 ;①
;① 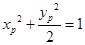 ;②
;②
 ;③
11分
;③
11分
由①+②+③得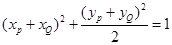
∴ 满足椭圆
满足椭圆 的方程,命题得证. 13分
的方程,命题得证. 13分
考点:1.抛物线和椭圆的方程;(2)直线与抛物线的位置关系;(3)向量的坐标运算.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:高中数学 来源:2012-2013学年湖北省黄冈市高三下学期6月适应性考试文科数学试卷(解析版) 题型:解答题
已知抛物线 的焦点
的焦点 以及椭圆
以及椭圆 的上、下焦点及左、右顶点均在圆
的上、下焦点及左、右顶点均在圆 上.
上.
(1)求抛物线 和椭圆
和椭圆 的标准方程;
的标准方程;
(2)过点 的直线交抛物线
的直线交抛物线 于
于 两不同点,交
两不同点,交 轴于点
轴于点 ,已知
,已知 ,则
,则
是否为定值?若是,求出其值;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖北省黄冈市高三6月适应性考试理科A数学试卷(解析版) 题型:解答题
已知抛物线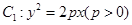 的焦点
的焦点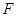 以及椭圆
以及椭圆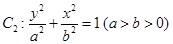 的上、下焦点及左、右顶点均在圆
的上、下焦点及左、右顶点均在圆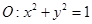 上.
上.
(1)求抛物线 和椭圆
和椭圆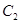 的标准方程;
的标准方程;
(2)过点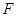 的直线交抛物线
的直线交抛物线 于
于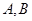 两不同点,交
两不同点,交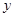 轴于点
轴于点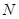 ,已知
,已知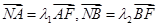 ,求
,求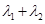 的值;
的值;
(3)直线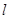 交椭圆
交椭圆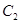 于
于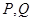 两不同点,
两不同点,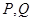 在
在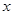 轴的射影分别为
轴的射影分别为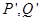 ,
,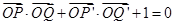 ,若点
,若点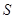 满足
满足 ,证明:点
,证明:点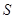 在椭圆
在椭圆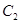 上.
上.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖北省黄冈市高三6月适应性考试文科A数学试卷(解析版) 题型:解答题
已知抛物线 的焦点
的焦点 以及椭圆
以及椭圆 的上、下焦点及左、右顶点均在圆
的上、下焦点及左、右顶点均在圆 上.
上.
(1)求抛物线 和椭圆
和椭圆 的标准方程;
的标准方程;
(2)过点 的直线交抛物线
的直线交抛物线 于
于 两不同点,交
两不同点,交 轴于点
轴于点 ,已知
,已知 ,则
,则 是否为定值?若是,求出其值;若不是,说明理由.
是否为定值?若是,求出其值;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源:2011年山东省青岛市高考模拟练习题(一)数学(理) 题型:解答题
(本小题满分14分)已知抛物线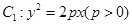 的焦点
的焦点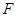 以及椭圆
以及椭圆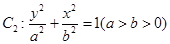 的上、下焦点及左、右顶点均在圆
的上、下焦点及左、右顶点均在圆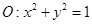 上.
上.
(Ⅰ)求抛物线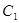 和椭圆
和椭圆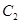 的标准方程;
的标准方程;
(Ⅱ)过点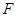 的直线交抛物线
的直线交抛物线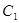 于
于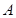 、
、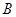 两不同点,交
两不同点,交 轴于点
轴于点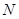 ,已知
,已知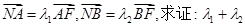 为定值.
为定值.
(Ⅲ)直线 交椭圆
交椭圆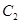 于
于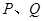 两不同点,
两不同点,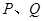 在
在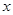 轴的射影分别为
轴的射影分别为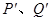 ,
, ,若点
,若点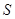 满足:
满足: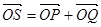 ,证明:点
,证明:点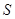 在椭圆
在椭圆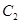 上.
上.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com