设集合A=(-∞,-2]∪[3,+∞),关于x的不等式(x-2a)(x+a)>0的解集为B(其中a<0).
(1)求集合B;
(2)设p:x∈A,q:x∈B,且?p是?q的必要不充分条件,求实数a的取值范围.
解:(1)∵a<0
∴若(x-2a)(x+a)>0
则x<2a,或x>-a
又∵不等式(x-2a)(x+a)>0的解集为B
∴B=(-∞,2a)∪(-a,+∞);
(2)∵p:x∈A,q:x∈B,且?p是?q的必要不充分条件,
∴A?B
又∵A=(-∞,-2]∪[3,+∞),
即
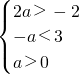
解得:-1<a<0
分析:(1)由已知中a<0,我们可以判断出对应方程(x-2a)(x+a)=0的两个根2a与-a大小,进而得到不等式(x-2a)(x+a)>0的解集B.
(2)根据(1)中结论,及p:x∈A,q:x∈B,且?p是?q的必要不充分条件,根据集合法判断充要条件的方法,我们易判断出集合A,B的包含关系,进而构造出关于a的不等式组,解不等式组,即可得到答案.
点评:本题考查的知识点是充要条件的判定,集合关系中参数取值问题,一元二次不等式的解法,其中(2)中易忽略a<0的限制,而错解为a>-1.



 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案