
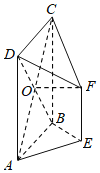
【题目】如图,在五面体![]() 中,侧面
中,侧面![]() 是正方形,
是正方形,![]() 是等腰直角三角形,点
是等腰直角三角形,点![]() 是正方形
是正方形![]() 对角线的交点,
对角线的交点,![]() 且
且![]() .
.
(1)证明:![]() 平面
平面![]() .
.
(2)若侧面![]() 与底面
与底面![]() 垂直,求五面体
垂直,求五面体![]() 的体积
的体积
科目:高中数学 来源: 题型:
【题目】给定数列![]() ,若满足
,若满足![]() (
(![]() 且
且![]() ),对于任意的
),对于任意的![]() ,都有
,都有![]() ,则称数列
,则称数列![]() 为“指数型数列”.
为“指数型数列”.
(1)已知数列![]() 的通项公式为
的通项公式为![]() ,试判断数列
,试判断数列![]() 是不是“指数型数列”;
是不是“指数型数列”;
(2)已知数列![]() 满足
满足![]() ,
,![]() ,证明数列
,证明数列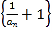 为等比数列,并判断数列
为等比数列,并判断数列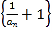 是否为“指数型数列”,若是给出证明,若不是说明理由;
是否为“指数型数列”,若是给出证明,若不是说明理由;
(3)若数列![]() 是“指数型数列”,且
是“指数型数列”,且![]() ,证明数列
,证明数列![]() 中任意三项都不能构成等差数列.
中任意三项都不能构成等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“纹样”是中国艺术宝库的瑰宝,“火纹”是常见的一种传统纹样,为了测算某火纹纹样(如图阴影部分所示)的面积,作一个边长为3的正方形将其包含在内,并向该正方形内随机投掷2000个点,己知恰有800个点落在阴影部分,据此可估计阴影部分的面积是

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学为了丰富学生的课外文体活动,分别开设了阅读、书法、绘画等文化活动;跑步、游泳、健身操等体育活动.该中学共有高一学生300名,要求每位学生必须选择参加其中一项活动,现对高一学生的性别、学习积极性及选择参加的文体活动情况进行统计,得到数据如下:

(1)在选择参加体育活动的学生中按性别分层抽取6名,再从这6名学生中抽取2人了解家庭情况,求2人中至少有1名女生的概率;
(2)是否有99.9%的把握认为学生的学习积极性与选择参加文化活动有关?请说明你的理由.
附:参考公式:![]() ,其中
,其中![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:若函数![]() 的导函数
的导函数![]() 是奇函数(
是奇函数(![]() ),则称函数
),则称函数![]() 是“双奇函数” .函数
是“双奇函数” .函数![]() .
.
(1)若函数![]() 是“双奇函数”,求实数
是“双奇函数”,求实数![]() 的值;
的值;
(2)假设![]() .
.
(i)在(1)的条件下,讨论函数![]() 的单调性;
的单调性;
(ii)若![]() ,讨论函数
,讨论函数![]() 的极值点.
的极值点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (
(![]() )的焦距为4,其短轴的两个端点与长轴的一个端点构成正三角形.
)的焦距为4,其短轴的两个端点与长轴的一个端点构成正三角形.
(1)求椭圆C的标准方程;
(2)设F为椭圆C的左焦点,T为直线![]() 上任意一点,过F作TF的垂线交椭圆C于点P,Q.
上任意一点,过F作TF的垂线交椭圆C于点P,Q.
(i)证明:OT平分线段PQ(其中O为坐标原点);
(ii)当![]() 最小时,求点T的坐标.
最小时,求点T的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
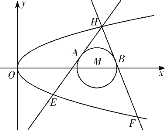
【题目】如图,已知抛物线![]() 和
和![]() ,过抛物线
,过抛物线![]() 上一点
上一点![]() 作两条直线与
作两条直线与![]() 分别相切于
分别相切于![]() 两点,分别交抛物线于
两点,分别交抛物线于![]() 两点.
两点.
(1)当![]() 的角平分线垂直
的角平分线垂直![]() 轴时,求直线
轴时,求直线![]() 的斜率;
的斜率;
(2)若直线![]() 在
在![]() 轴上的截距为
轴上的截距为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,焦距为
,焦距为![]() ,直线
,直线![]() :
:![]() 与椭圆相交于
与椭圆相交于![]() 、
、![]() 两点,
两点,![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 在椭圆上.斜率为
在椭圆上.斜率为![]() 的直线
的直线![]() 与线段
与线段![]() 相交于点
相交于点![]() ,与椭圆相交于
,与椭圆相交于![]() 、
、![]() 两点.
两点.

(1)求椭圆的标准方程;
(2)求四边形![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com