
【题目】已知定义在![]() 上的函数
上的函数![]() 满足:对任意
满足:对任意![]() 都有
都有![]() .
.
(1)求证:函数![]() 是奇函数;
是奇函数;
(2)如果当![]() 时,有
时,有![]() ,试判断
,试判断![]() 在
在![]() 上的单调性,并用定义证明你的判断;
上的单调性,并用定义证明你的判断;
(3)在(2)的条件下,若![]() 对满足不等式
对满足不等式![]() 的任意
的任意![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1)证明见解析(2)函数![]() 在
在![]() 上为增函数,证明见解析(3)
上为增函数,证明见解析(3)![]()
【解析】
(1)先分析定义域是否关于原点对称,再赋值求![]() ,令
,令![]() 即可求证(2)先判断
即可求证(2)先判断![]() 在
在![]() 上为增函数,再根据定义证明在
上为增函数,再根据定义证明在![]() 上是奇函数,根据奇函数性质知
上是奇函数,根据奇函数性质知![]() 在
在![]() 上为增函数(3)根据(2)可得不等式
上为增函数(3)根据(2)可得不等式![]() 的解,
的解,![]() 在此范围恒成立,分离参数即可求解.
在此范围恒成立,分离参数即可求解.
(1)函数![]() 的定义域
的定义域![]() 关于原点对称,令
关于原点对称,令![]() ,可得
,可得![]() ,
,
所以![]() ,令
,令![]() ,则
,则![]() ,即
,即![]() ,所以函数为奇函数.
,所以函数为奇函数.
(2)函数![]() 在
在![]() 上为增函数.
上为增函数.
证明如下:
设![]() 且
且![]() ,则
,则![]()
![]() ,
,
因为![]() 时,有
时,有![]() ,
,
所以![]() ,
,
故![]()
即![]() ,
,
所以函数![]() 在
在![]() 上是增函数,
上是增函数,
根据奇函数的性质知函数![]() 在
在![]() 上是增函数,
上是增函数,
故![]() 在
在![]() 上为增函数.
上为增函数.
(3)因为![]() ,
,
所以![]() ,
,
因为![]() 在
在![]() 上为增函数,
上为增函数,
所以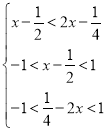 ,解得
,解得![]() .
.
即当![]() 时,
时,![]() 恒成立,
恒成立,
所以![]() 在
在![]() 上恒成立,
上恒成立,
而![]() ,
,
所以只需![]() ,
,
故![]() 的取值范围为
的取值范围为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知边长为 ![]() 的菱形ABCD中,∠BAD=60°,沿对角线BD折成二面角A﹣BD﹣C为120°的四面体ABCD,则四面体的外接球的表面积为( )
的菱形ABCD中,∠BAD=60°,沿对角线BD折成二面角A﹣BD﹣C为120°的四面体ABCD,则四面体的外接球的表面积为( )
A.25π
B.26π
C.27π
D.28π
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产的某批产品的销售量![]() 万件(生产量与销售量相等)与促销费用
万件(生产量与销售量相等)与促销费用![]() 万元满足
万元满足![]() (其中
(其中![]() ,
,![]() 为正常数).已知生产该批产品还需投入成本
为正常数).已知生产该批产品还需投入成本![]() 万元(不含促销费用),产品的销售价格定为
万元(不含促销费用),产品的销售价格定为![]() 元/件
元/件
(1)将该产品的利润![]() 万元表示为促销费用
万元表示为促销费用![]() 万元的函数;(注:利润=销售收入-促销费-投入成本)
万元的函数;(注:利润=销售收入-促销费-投入成本)
(2)当促销费用投入多少万元时,该公司的利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(12分)已知函数f(x)=![]()
(1)判断函数在区间[1,+∞)上的单调性,并用定义证明你的结论.
(2)求该函数在区间[1,4]上的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax﹣lnx,a∈R.
(1)求函数f(x)的单调区间;
(2)当x∈(0,e]时,求g(x)=e2x﹣lnx的最小值;
(3)当x∈(0,e]时,证明:e2x﹣lnx﹣ ![]() >
> ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为调查某地区老人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如下:
性别 是否需要志愿者 | 男 | 女 |
需要 | 40 | 30 |
不需要 | 160 | 270 |
(1)估计该地区老年人中,需要志愿者提供帮助的老年人的比例;
(2)请根据上面的数据分析该地区的老年人需要志愿者提供帮助与性别有关吗
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xlnx,g(x)= ![]() (其中a∈R)
(其中a∈R)
(1)求函数f(x)的极值;
(2)设函数h(x)=f′(x)+g(x)﹣1,试确定h(x)的单调区间及最值;
(3)求证:对于任意的正整数n,均有 ![]() >
> ![]() 成立.(注:e为自然对数的底数)
成立.(注:e为自然对数的底数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com