
分析 A∩B中有且仅有一个元素?两个方程联立得到的二次方程有且仅有一个根;通过对判别式分类讨论,结合二次方程相应的函数列出满足条件的不等式,求出m的范围.
解答 解:将y=x+2代入y=-x2+(m-1)x-1,
消去y得:x+2=-x2+(m-1)x-1,即x2-(2-m)x+3=0,1≤x≤4
∵A∩B是单元素集,
∴分两种情况考虑:
①方程有两个相等的实数根,即△=0,且-$\frac{-(2-m)}{2}$=$\frac{2-m}{2}$∈[1,4],
即(m-2)2-12=0,且-6≤m≤0
解得:m=2-2$\sqrt{3}$或m=2+2$\sqrt{3}$(舍去),
②△>0时,只有一根在[1,4]上,
设f(x)=x2-(2-m)x+3,
∴f(0)=3>0,两根之积为3>0,
∴$\left\{\begin{array}{l}{f(1)≥0}\\{f(4)≤0}\end{array}\right.$,即$\left\{\begin{array}{l}{1-(2-m)+3≥0}\\{16-4(2-m)+3≤0}\end{array}\right.$,
即$\left\{\begin{array}{l}{m≥-2}\\{m≤-\frac{11}{4}}\end{array}\right.$,此时无解,
综上m=2-2$\sqrt{3}$.
点评 此题考查了交集及其运算,利用了分类讨论的思想,弄清题意是解本题的关键将函数转化为一元二次方程根的分布问题是解决本题的关键.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
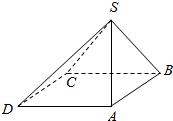 如图,四棱锥S-ABCD中,底面ABCD为菱形,侧面SBC⊥底面ABCD,已知∠ABC=60°,AB=SB=SC=2.
如图,四棱锥S-ABCD中,底面ABCD为菱形,侧面SBC⊥底面ABCD,已知∠ABC=60°,AB=SB=SC=2.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2,0)∪(0,2] | B. | [-2,2] | C. | (-1,2] | D. | (-1,0)∪(0,2] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com