
【题目】如图,已知矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 的中点,将
的中点,将![]() 沿着
沿着![]() 折起,使得
折起,使得![]() .
.
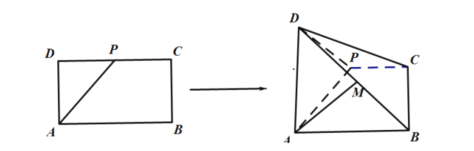
(1)求证:![]() ;
;
(2)若![]() 是
是![]() 的中点,求直线
的中点,求直线![]() 与平面
与平面![]() 的所成角的正弦值.
的所成角的正弦值.
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:高中数学 来源: 题型:
【题目】下图是某地5月1日至15日日平均温度变化的折线图,日平均温度高于20度低于27度时适宜户外活动,某人随机选择5月1日至5月14日中的某一天到达该地停留两天(包括到达当日).
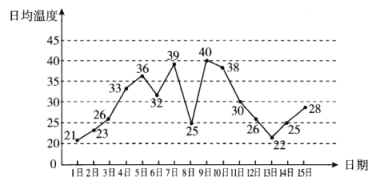
(1)求这15天日平均温度的极差和均值;
(2)求此人停留期间只有一天的日平均温度适宜户外活动的概率;
(3)由折线图判断从哪天开始连续三天日平均温度的方差最大?(写出结论,不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 分别为椭圆
分别为椭圆![]() 的左、右焦点,点
的左、右焦点,点![]() 在椭圆
在椭圆![]() 上,且点
上,且点![]() 和
和![]() 关于点
关于点![]() 对称.
对称.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)过右焦点![]() 的直线
的直线![]() 与椭圆相交于
与椭圆相交于![]() 两点,过点
两点,过点![]() 且平行于
且平行于![]() 的直线与椭圆交于另一点
的直线与椭圆交于另一点![]() ,问是否存在直线
,问是否存在直线![]() ,使得四边形
,使得四边形![]() 的对角线互相平分?若存在,求出
的对角线互相平分?若存在,求出![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 中,角A,B,C的对边分别为a,b,c,
中,角A,B,C的对边分别为a,b,c,![]()
(1)若![]() 还同时满足下列四个条件中的三个:①
还同时满足下列四个条件中的三个:①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() 的面积
的面积![]() ,请指出这三个条件,并说明理由;
,请指出这三个条件,并说明理由;
(2)若![]() ,求
,求![]() 周长L的取值范围.
周长L的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次运动会上,某单位派出了由6名主力队员和5名替补队员组成的代表队参加比赛.
(1)如果随机抽派5名队员上场比赛,将主力队员参加比赛的人数记为![]() ,求随机变量
,求随机变量![]() 的数学期望;
的数学期望;
(2)若主力队员中有2名队员在练习比赛中受轻伤,不宜同时上场;替补队员中有2名队员身材相对矮小,也不宜同时上场,那么为了场上参加比赛的5名队员中至少有3名主力队员,教练员有多少种组队方案?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为培养学生对传统文化的兴趣,某校从理科甲班抽取60人,从文科乙班抽取50人参加传统文化知识竞赛.
(1)根据题目条件完成下边![]() 列联表,并据此判断是否有99%的把握认为学生的传统文化知识竞赛成绩优秀与文理分科有关.
列联表,并据此判断是否有99%的把握认为学生的传统文化知识竞赛成绩优秀与文理分科有关.
优秀人数 | 非优秀人数 | 总计 | |
甲班 | |||
乙班 | 20 | ||
总计 | 60 |
(2)现已知![]() ,
,![]() ,
,![]() 三人获得优秀的概率分别为
三人获得优秀的概率分别为![]() ,
,![]() ,
,![]() ,设随机变量
,设随机变量![]() 表示
表示![]() ,
,![]() ,
,![]() 三人中获得优秀的人数,求
三人中获得优秀的人数,求![]() 的分布列及期望
的分布列及期望![]() .
.
附: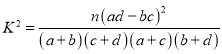 ,
,![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 | 0.005 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,过曲线![]() 外的一点
外的一点![]() (其中
(其中![]() ,
,![]() 为锐角)作平行于
为锐角)作平行于![]() 的直线
的直线![]() 与曲线分别交于
与曲线分别交于![]() .
.
(Ⅰ) 写出曲线![]() 和直线
和直线![]() 的普通方程(以极点为原点,极轴为
的普通方程(以极点为原点,极轴为![]() 轴的正半轴建系);
轴的正半轴建系);
(Ⅱ)若![]() 成等比数列,求
成等比数列,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com