

| ξ | 1 | 2 | |
| P(ξ) | 0.05 | 0.35 | 0.60 |


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
 18、
18、查看答案和解析>>
科目:高中数学 来源: 题型:
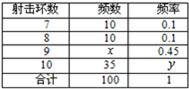
甲乙两运动员进行射击训练,已知他们击中目标的环数都稳定在7,8,9,10环,且每次射击成绩互不影响,射击环数的频率分布表如下,
甲运动员
| 射击环数 | 频数 | 频率 |
| 7 | 10 | 0.1 |
| 8 | 10 | 0.1 |
| 9 |
| 0.45 |
| 10 | 35 |
|
| 合计 | 100 | 1 |
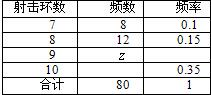
乙运动员
| 射击环数 | 频数 | 频率 |
| 7 | 8 | 0.1 |
| 8 | 12 | 0.15 |
| 9 |
| |
| 10 | 0.35 | |
| 合计 | 80 | 1 |
若将频率视为概率,回答下列问题,
(1)求甲运动员击中10环的概率
(2)求甲运动员在3次射击中至少有一次击中9环以上(含9环)的概率
(3)若甲运动员射击2次,乙运动员射击1次,![]() 表示这3次射击中击中9环以上(含9环)的次数,求
表示这3次射击中击中9环以上(含9环)的次数,求![]() 的分布列及
的分布列及![]() .
.
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
甲乙两运动员进行射击训练,已知他们击中目标的环数都稳定在7,8,9,10环,且每次射击成绩互不影响,射击环数的频率分布表如![]() 下,
下,
甲运动员
| 射击环数 | 频数 | 频率 |
| 7 | 10 | 0.1 |
| 8 | 10 | 0.1 |
| 9 |
| 0.45 |
| 10 | 35 |
|
| 合计 |
| 1 |
乙运动员
| 射击环数 | 频数 | 频率 |
| 7 | 8 | 0.1 |
| 8 | 12 | 0.15 |
| 9 |
| |
| 10 | 0.35 | |
| 合计 | 80 | 1 |
若将频率视为概率,回答下列问题,
(1)求甲运动员击中10环的概率
(2)求甲运动员在3次射击中至少有一次击中9环以上(含9环)的概率
(3)若甲运动员射击2次,乙运动员射击1次,![]() 表示这3次射击中击中9环以上(含9环)的次数,求
表示这3次射击中击中9环以上(含9环)的次数,求![]() 的分布列及
的分布列及![]() .
.
查看答案和解析>>
科目:高中数学 来源:2013年广东省东莞市高考数学模拟试卷(理科)(解析版) 题型:解答题


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com