
���� �����ж���������y=kax��k��0��a��1����$y=p{x^{\frac{1}{2}}}+q��p��0��$�ڣ�0��+�ޣ��ĵ����ԣ�˵������ģ��y=kax��k��0��a��1���ʺ�Ҫ��Ȼ���г������飬��⼴�ɣ�
�������� x=0ʱ��$y=\frac{32}{3}•{��{\frac{3}{2}}��^0}=\frac{32}{3}$��Ԫ����������������$\frac{32}{3}{m^2}$���г�����ʽת����⼴�ɣ�
��� ��С�����֣�12�֣���
�⣺������������y=kax��k��0��a��1����$y=p{x^{\frac{1}{2}}}+q��p��0��$�ڣ�0��+�ޣ��϶���������������x�����ӣ�����y=kax��k��0��a��1����ֵ���ӵ�Խ��Խ�죬������$y=p{x^{\frac{1}{2}}}+q��p��0��$��ֵ���ӵ�Խ��Խ����
���ڷ������ں��е������ٶ�Խ��Խ�죬���Ժ���ģ��y=kax��k��0��a��1���ʺ�Ҫ��
�������֪��x=2ʱ��y=24��x=3ʱ��y=36������$\left\{{\begin{array}{l}{k{a^2}=24}\\{k{a^3}=36}\end{array}}\right.$
���$\left\{{\begin{array}{l}{k=\frac{32}{3}}\\{a=\frac{3}{2}}\end{array}}\right.$
���Ըú���ģ�͵Ľ���ʽ��$y=\frac{32}{3}•{��{\frac{3}{2}}��^x}$��x��N*����
���� x=0ʱ��$y=\frac{32}{3}•{��{\frac{3}{2}}��^0}=\frac{32}{3}$��
����Ԫ����������������$\frac{32}{3}{m^2}$��
��$\frac{32}{3}•{��{\frac{3}{2}}��^x}��10��\frac{32}{3}$��${��{\frac{3}{2}}��^x}��10$��
����$x��{log_{\frac{3}{2}}}10=\frac{lg10}{{1g\frac{3}{2}}}=\frac{1}{lg3-lg2}$��
��Ϊ$\frac{1}{lg3-lg2}=\frac{1}{0.4770-0.3010}��5.7$������x��6��
���Է��������������Ԫ��������������10�����ϵ���С�·���6�·ݣ�
���� ��С�⿼����ѧ��ģ���������������������������ͽ�������������������ѧӦ����ʶ



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
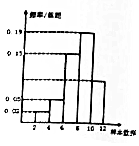 ��һ������Ϊ200����������Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ������������Ƶ�ʷֲ�ֱ��ͼ���ƣ�����������������[10��12]�ڵ�Ƶ��Ϊ36��
��һ������Ϊ200����������Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ������������Ƶ�ʷֲ�ֱ��ͼ���ƣ�����������������[10��12]�ڵ�Ƶ��Ϊ36���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3 | B�� | $7+4\sqrt{3}$ | C�� | $\frac{1}{3}$ | D�� | $3+2\sqrt{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y=x-1 | B�� | y=��$\frac{1}{2}$��x | C�� | y=x3 | D�� | $y={log_{\frac{1}{2}}}x$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
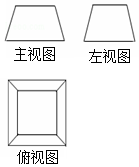
| A�� | ��̨ | B�� | �� | C�� | ���� | D�� | �������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
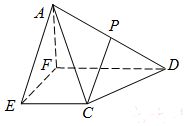 ��ͼ��������A-CDFE�У�����CDFE��ֱ�����Σ�CE��DF��EF��EC��$CE=\frac{1}{2}DF$��AF��ƽ��CDFE��PΪAD�е㣮
��ͼ��������A-CDFE�У�����CDFE��ֱ�����Σ�CE��DF��EF��EC��$CE=\frac{1}{2}DF$��AF��ƽ��CDFE��PΪAD�е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��e��+�ޣ� | B�� | $��\frac{1}{e}��1��$ | C�� | ��2��3�� | D�� | ��e��+�ޣ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| x | 0 | 1 | 2 |
| y | a | $\frac{20}{3}$ | $\frac{40}{9}$ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com