
【题目】已知函数f(x)![]() a2x(k∈R,a>0,e为自然对数的底数),且曲线f(x)在点(1,f(1))处的切线的斜率为e2﹣a2.
a2x(k∈R,a>0,e为自然对数的底数),且曲线f(x)在点(1,f(1))处的切线的斜率为e2﹣a2.
(1)求实数k的值,并讨论函数f(x)的单调性;
(2)设函数g(x)![]() ,若对x1∈(0,+∞),x2∈R,使不等式f(x2)≤g(x1)﹣1成立,求实数a的取值范围.
,若对x1∈(0,+∞),x2∈R,使不等式f(x2)≤g(x1)﹣1成立,求实数a的取值范围.
【答案】(1)k=2,见解析(2)0<a![]() .
.
【解析】
(1)求出![]() ,由已知求出
,由已知求出![]() ,
,![]() ,求出
,求出![]() 的范围,即可得出结论;
的范围,即可得出结论;
(2)对x1∈(0,+∞),x2∈R,使不等式f(x2)≤g(x1)﹣1成立,转化为![]() 由(1)求出
由(1)求出![]() ,用导数法求出
,用导数法求出![]() ,即可求解.
,即可求解.
(1)![]() ,f'(1)
,f'(1)![]() ,
,
得![]() ,故k=2,a>0,所以
,故k=2,a>0,所以![]() =e2x﹣a2=e2x﹣e2lna,
=e2x﹣a2=e2x﹣e2lna,
当x∈(﹣∞,lna)时,![]() <0,f(x)递减;
<0,f(x)递减;
当x∈(lna,+∞)时,![]() ,f(x)递增;
,f(x)递增;
![]() 单调递减区间是
单调递减区间是![]() ,单调递增区间是
,单调递增区间是![]()
(2)根据(1)当x∈R时,f(x)有最小值为
f(lna)![]() ,
,
g(x)![]() ,
,
![]()
![]() ,
,
令h(x)=x2ex+lnx,显然函数在(0,+∞)单调递增,
由h(![]() )
)![]() ,h(1)>0,
,h(1)>0,
故h(x)在(![]() ,1)存在唯一的零点m,使得h(m)=0,
,1)存在唯一的零点m,使得h(m)=0,
即m2em+lnm=0,当x∈(0,m)时,g(x)递减;
x∈(m,+∞)时,g(x)递增;
故g(m)为g(x)的最小值,
g(m)﹣1![]()
![]() ,
,
对于y![]() 与h(m)都单调递增,
与h(m)都单调递增,
且当![]() 时,
时,![]() 0成立,
0成立,
所以g(m)﹣1=0,
根据题意,![]() 0,即
0,即![]() ,
,
故a![]() ,故0<a
,故0<a![]() .
.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】某工厂的某种产品成箱包装,每箱200件,每一箱产品在交付用户之前要对产品作检验,如检验出不合格品,则更换为合格品.检验时,先从这箱产品中任取20件作检验,再根据检验结果决定是否对余下的所有产品作检验,设每件产品为不合格品的概率都为![]() ,且各件产品是否为不合格品相互独立.
,且各件产品是否为不合格品相互独立.
(1)记20件产品中恰有2件不合格品的概率为![]() ,求
,求![]() 的最大值点
的最大值点![]() .
.
(2)现对一箱产品检验了20件,结果恰有2件不合格品,以(1)中确定的![]() 作为
作为![]() 的值.已知每件产品的检验费用为2元,若有不合格品进入用户手中,则工厂要对每件不合格品支付25元的赔偿费用.
的值.已知每件产品的检验费用为2元,若有不合格品进入用户手中,则工厂要对每件不合格品支付25元的赔偿费用.
(i)若不对该箱余下的产品作检验,这一箱产品的检验费用与赔偿费用的和记为![]() ,求
,求![]() ;
;
(ii)以检验费用与赔偿费用和的期望值为决策依据,是否该对这箱余下的所有产品作检验?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列的定义为:在一个数列中,从第二项起,如果每一项与它的前一项的差都为同一个常数,那么这个数叫做等差数列,这个常数叫做该数列的公差.类比等差数列的定义给出“等和数列”的定义:_____________________________________;已知数列![]() 是等和数列,且
是等和数列,且![]() ,公和为
,公和为![]() ,那么
,那么![]() 的值为____________.这个数列的前
的值为____________.这个数列的前![]() 项和
项和![]() 的计算公式为_____________________________________.
的计算公式为_____________________________________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() :
:![]() ,
,![]() ,
,![]() ,…,
,…,![]() 为1,2,3,…,
为1,2,3,…,![]() 的一个排列,若
的一个排列,若![]() 互不相同,则称数列
互不相同,则称数列![]() 具有性质
具有性质![]() .
.
(1)若![]() ,且
,且![]() ,写出具有性质
,写出具有性质![]() 的所有数列
的所有数列![]() ;
;
(2)若数列![]() 具有性质
具有性质![]() ,证明:
,证明:![]() ;
;
(3)当![]() 时,分别判断是否存在具有性质
时,分别判断是否存在具有性质![]() 的数列
的数列![]() ?请说明理由.
?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)![]() 若方程2[f(x)]2﹣5tf(x)+3t2=0恰有4个不同的实根,则实数t的取值范围为(参考数据:ln2≈0.6931)( )
若方程2[f(x)]2﹣5tf(x)+3t2=0恰有4个不同的实根,则实数t的取值范围为(参考数据:ln2≈0.6931)( )
A.(![]() ,
,![]() )
)
B.(![]() ,
,![]() )
)
C.(![]() ,2﹣2ln2)∪(
,2﹣2ln2)∪(![]() ,1)
,1)
D.(![]() ,2﹣1n2)
,2﹣1n2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某学校高三年级共1000名男生中随机抽取50人测量身高,据测量,被测学生身高全部介于![]() 到
到![]() 之间,将测量结果按如下方式分成八组:第一组
之间,将测量结果按如下方式分成八组:第一组![]() ,第二组
,第二组![]() ,…,第八组
,…,第八组![]() .如图是按上述分组方法得到的频率分布直方图的一部分.其中第六组、第七组、第八组人数依次构成等差数列.
.如图是按上述分组方法得到的频率分布直方图的一部分.其中第六组、第七组、第八组人数依次构成等差数列.
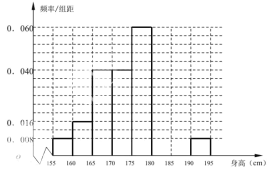
(1)求第六组、第七组的频率,并估计高三年级全体男生身高在![]() 以上(含
以上(含![]() )的人数;
)的人数;
(2)学校决定让这五十人在运动会上组成一个高旗队,在这五十人中要选身高在![]() 以上(含
以上(含![]() )的两人作为队长,求这两人在同一组的概率.
)的两人作为队长,求这两人在同一组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某农场有一块农田,如图所示,它的边界由圆O的一段圆弧![]() (P为此圆弧的中点)和线段MN构成.已知圆O的半径为40米,点P到MN的距离为50米.现规划在此农田上修建两个温室大棚,大棚Ⅰ内的地块形状为矩形ABCD,大棚Ⅱ内的地块形状为
(P为此圆弧的中点)和线段MN构成.已知圆O的半径为40米,点P到MN的距离为50米.现规划在此农田上修建两个温室大棚,大棚Ⅰ内的地块形状为矩形ABCD,大棚Ⅱ内的地块形状为![]() ,要求
,要求![]() 均在线段
均在线段![]() 上,
上,![]() 均在圆弧上.设OC与MN所成的角为
均在圆弧上.设OC与MN所成的角为![]() .
.
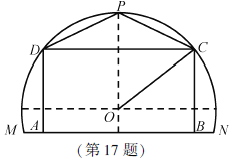
(1)用![]() 分别表示矩形
分别表示矩形![]() 和
和![]() 的面积,并确定
的面积,并确定![]() 的取值范围;
的取值范围;
(2)若大棚Ⅰ内种植甲种蔬菜,大棚Ⅱ内种植乙种蔬菜,且甲、乙两种蔬菜的单位面积年产值之比为![]() .求当
.求当![]() 为何值时,能使甲、乙两种蔬菜的年总产值最大.
为何值时,能使甲、乙两种蔬菜的年总产值最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
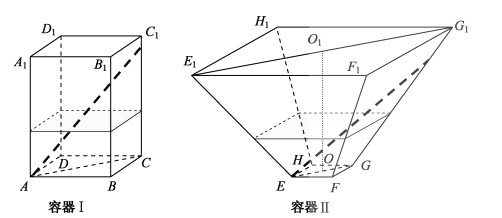
【题目】如图,水平放置的正四棱柱形玻璃容器Ⅰ和正四棱台形玻璃容器Ⅱ的高均为32cm,容器Ⅰ的底面对角线AC的长为10![]() cm,容器Ⅱ的两底面对角线EG,E1G1的长分别为14cm和62cm. 分别在容器Ⅰ和容器Ⅱ中注入水,水深均为12cm. 现有一根玻璃棒l,其长度为40cm.(容器厚度、玻璃棒粗细均忽略不计)
cm,容器Ⅱ的两底面对角线EG,E1G1的长分别为14cm和62cm. 分别在容器Ⅰ和容器Ⅱ中注入水,水深均为12cm. 现有一根玻璃棒l,其长度为40cm.(容器厚度、玻璃棒粗细均忽略不计)
(1)将l放在容器Ⅰ中,l的一端置于点A处,另一端置于侧棱CC1上,求l没入水中部分的长度;
(2)将l放在容器Ⅱ中,l的一端置于点E处,另一端置于侧棱GG1上,求l没入水中部分的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com