
【题目】已知质点P绕点M逆时针做匀速圆周运动(如图1),质点P相对于水平直线l的位置用y(米)表示,质点在l上方时,y为正,反之,y为负,![]() 是质点与直线l的距离,位置y与时间t(秒)之间的关系为
是质点与直线l的距离,位置y与时间t(秒)之间的关系为![]() (其中
(其中![]() ,
,![]() ,
,![]() )其图象如图2所示.
)其图象如图2所示.

(1)写出质点P运动的圆形轨道半径及从初始位置到最高点所需要的时间;
(2)求![]() 的解析式,并指出质点P第二次出现在直线l上的时刻.
的解析式,并指出质点P第二次出现在直线l上的时刻.
科目:高中数学 来源: 题型:
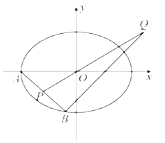
【题目】如图,在平面直角坐标系xoy中,椭圆C:![]() 的左顶点为A,点B是椭圆C上异于左、右顶点的任一点,P是AB的中点,过点B且与AB垂直的直线与直线OP交于点Q,已知椭圆C的离心率为
的左顶点为A,点B是椭圆C上异于左、右顶点的任一点,P是AB的中点,过点B且与AB垂直的直线与直线OP交于点Q,已知椭圆C的离心率为![]() ,点A到右准线的距离为6.
,点A到右准线的距离为6.
(1)求椭圆C的标准方程;
(2)设点Q的横坐标为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校实行选科走班制度,张毅同学的选择是物理、生物、政治这三科,且物理在A层班级,生物在B层班级,该校周一上午课程安排如表所示,张毅选择三个科目的课各上一节,另外一节上自习,则他不同的选课方法有( )
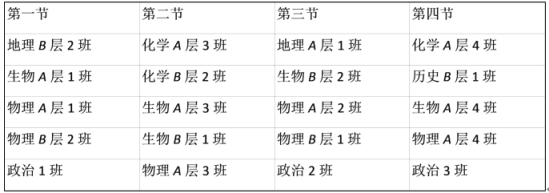
A.8种B.10种C.12种D.14种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 在
在![]() 处取得极值.
处取得极值.
(Ⅰ)求函数![]() 的解析式;
的解析式;
(Ⅱ)求证:对于区间![]() 上任意两个自变量的值
上任意两个自变量的值![]() ,都有
,都有![]() ;
;
(Ⅲ)若过点![]() 可作曲线
可作曲线![]() 的三条切线,求实数
的三条切线,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知公差不为零的等差数列{an)满足a1=5,且a3,a6,a11成等比数列.
(1)求数列{an}的通项公式;
(2)设bn=an·3n-1,求数列{bn}的前n项和Sn.
查看答案和解析>>
科目:高中数学 来源: 题型:
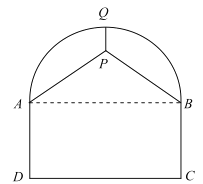
【题目】如图,某隧道的剖面图是由半圆及矩形![]() 组成,交通部门拟在隧道顶部安装通风设备(视作点
组成,交通部门拟在隧道顶部安装通风设备(视作点![]() ),为了固定该设备,计划除从隧道最高点
),为了固定该设备,计划除从隧道最高点![]() 处使用钢管垂直向下吊装以外,再在两侧自
处使用钢管垂直向下吊装以外,再在两侧自![]() 两点分别使用钢管支撑.已知道路宽
两点分别使用钢管支撑.已知道路宽![]() ,设备要求安装在半圆内部,所使用的钢管总长度为
,设备要求安装在半圆内部,所使用的钢管总长度为![]() .
.
(1)①设![]() ,将
,将![]() 表示为关于
表示为关于![]() 的函数;
的函数;
②设![]() ,将
,将![]() 表示为关于
表示为关于![]() 的函数;
的函数;
(2)请选用(1)中的一个函数关系式,说明如何设计,所用的钢管材料最省?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].
(1)求图中![]() 的值;
的值;
(2)根据频率分布直方图,估计这100名学生语文成绩的平均分,众数,中位数;
(3)若这100名学生语文成绩某些分数段的人数(![]() )与数学成绩相应分数段的人数(
)与数学成绩相应分数段的人数(![]() )之比如下表所示,求数学成绩在[50,90)之外的人数.
)之比如下表所示,求数学成绩在[50,90)之外的人数.
分数段 | [50,60) | [60,70) | [70,80) | [80,90) |
| 1:1 | 2:1 | 3:4 | 4:5 |

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用水清洗一份蔬菜上残留的农药,对用一定量的水清洗一次的效果作如下假定:用1个单位量的水可洗掉蔬菜上残留农药量的![]() ,用水越多洗掉的农药量也越多,但总还有农药残留在蔬菜上.设用
,用水越多洗掉的农药量也越多,但总还有农药残留在蔬菜上.设用![]() 单位量的水清洗一次以后,蔬菜上残留的农药量与本次清洗前残留的农药量之比为函数
单位量的水清洗一次以后,蔬菜上残留的农药量与本次清洗前残留的农药量之比为函数![]() .
.
(1)求![]() 的值,并解释其实际意义;
的值,并解释其实际意义;
(2)现有![]() 单位量的水,可以清洗一次,也可以把水平均分成2份后清洗两次,试问用哪种方案清洗后蔬菜上残留的农药量比较少?说明理由.
单位量的水,可以清洗一次,也可以把水平均分成2份后清洗两次,试问用哪种方案清洗后蔬菜上残留的农药量比较少?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com