
【题目】国内某知名连锁店分店开张营业期间,在固定的时间段内消费达到一定标准的顾客可进行一次抽奖活动,随着抽奖活动的有效开展,参与抽奖活动的人数越来越多,该分店经理对开业前![]() 天参加抽奖活动的人数进行统计,
天参加抽奖活动的人数进行统计, ![]() 表示开业第
表示开业第![]() 天参加抽奖活动的人数,得到统计表格如下:
天参加抽奖活动的人数,得到统计表格如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
经过进一步统计分析,发现![]() 与
与![]() 具有线性相关关系.
具有线性相关关系.
(1)若从这![]() 天中随机抽取两天,求至少有
天中随机抽取两天,求至少有![]() 天参加抽奖人数超过
天参加抽奖人数超过![]() 的概率;
的概率;
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并估计若该活动持续
,并估计若该活动持续![]() 天,共有多少名顾客参加抽奖.
天,共有多少名顾客参加抽奖.
参考公式: 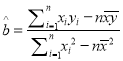 ,
, ![]() .
.
科目:高中数学 来源: 题型:
【题目】已知△ABC是斜三角形,内角A、B、C所对的边的长分别为a、b、c.若csinA= ![]() acosC.
acosC.
(1)求角C;
(2)若c= ![]() ,且sinC+sin(B﹣A)=5sin2A,求△ABC的面积.
,且sinC+sin(B﹣A)=5sin2A,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正四棱锥(底面为正方形,顶点在底面上的射影是底面的中心)S﹣ABCD的底面边长为2,高为2,E为边BC的中点,动点P在表面上运动,并且总保持PE⊥AC,则动点P的轨迹的周长为( )
A.![]()
B.![]()
C.3 ![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,半径为![]() 的圆形纸板内有一个相同圆心的半径为
的圆形纸板内有一个相同圆心的半径为![]() 的小圆,现将半径为
的小圆,现将半径为![]() 的一枚硬币抛到此纸板上,使整块硬币完全随机落在纸板内,则硬币与小圆无公共点的概率为( )
的一枚硬币抛到此纸板上,使整块硬币完全随机落在纸板内,则硬币与小圆无公共点的概率为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某教育机构随机某校20个班级,调查各班关注汉字听写大赛的学生人数,根据所得数据的茎叶图,以组距为5将数据分组成[0,5),[5,10),[10,15),[15,20),[20,25),[25,30),[30,35),[35,40]时,所作的频率分布直方图如图所示,则原始茎叶图可能是( ) 
A.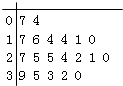
B.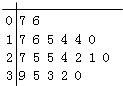
C.
D.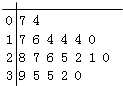
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为倡导全体学生为特困学生捐款,举行“一元钱,一片心,诚信用水”活动,学生在购水处每领取一瓶矿泉水,便自觉向捐款箱中至少投入一元钱.现统计了连续5天的售出和收益情况,如表:
售出水量x(单位:箱) | 7 | 6 | 6 | 5 | 6 |
收益y(单位:元) | 165 | 142 | 148 | 125 | 150 |
(1)求y关于x的线性回归方程;
(2)预测售出8箱水的收益是多少元?
附:回归直线的斜率和截距的最小二乘法估计公式分别为: ![]() =
= 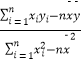 ,
, ![]() =
= ![]() ﹣
﹣ ![]()
![]() ,
,
参考数据:7×165+6×142+6×148+5×125+6×150=4420.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经销商经销某种农产品,在一个销售季度内,每售出![]() 该产品获利润500元,未售出的产品,每
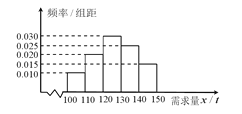
该产品获利润500元,未售出的产品,每![]() 亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直图,如图所示.经销商为下一个销售季度购进了
亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直图,如图所示.经销商为下一个销售季度购进了![]() 该农产品.以
该农产品.以![]() (
(![]() )表示下一个销售季度内的市场需求量,
)表示下一个销售季度内的市场需求量, ![]() (单位:元)表示下一个销售季度内经销该农产品的利润.
(单位:元)表示下一个销售季度内经销该农产品的利润.
(Ⅰ)将![]() 表示为
表示为![]() 的函数;
的函数;
(Ⅱ)根据直方图估计利润![]() 不少于57000元的概率.
不少于57000元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,已知 ![]() tanAtanB﹣tanA﹣tanB=
tanAtanB﹣tanA﹣tanB= ![]() .
.
(1)求∠C的大小;
(2)设角A,B,C的对边依次为a,b,c,若c=2,且△ABC是锐角三角形,求a2+b2的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
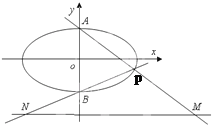
【题目】如图,已知椭圆![]() 的上、下顶点分别为A,B,点P在椭圆上,且异于点A,B,直线AP,BP与直线
的上、下顶点分别为A,B,点P在椭圆上,且异于点A,B,直线AP,BP与直线![]() 分别交于点M,N,
分别交于点M,N,
(1)设直线AP,BP的斜率分别为![]() ,求证:
,求证: ![]() 为定值;
为定值;
(2)求线段MN的长的最小值;
(3)当点P运动时,以MN为直径的圆是否经过某定点?请证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com