
【题目】已知函数f(x)满足f(x)=f( ![]() )且当x∈[
)且当x∈[ ![]() ,1]时,f(x)=lnx,若当x∈[
,1]时,f(x)=lnx,若当x∈[ ![]() ]时,函数g(x)=f(x)﹣ax与x轴有交点,则实数a的取值范围是( )
]时,函数g(x)=f(x)﹣ax与x轴有交点,则实数a的取值范围是( )
A.[﹣ ![]() ,0]
,0]
B.[﹣πlnπ,0]
C.[﹣ ![]() ,
, ![]() ]
]
D.[﹣ ![]() ,﹣
,﹣ ![]() ]
]
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】已知双曲线 C1: ![]() =1( a>0,b>0),圆 C2:x2+y2﹣2ax+
=1( a>0,b>0),圆 C2:x2+y2﹣2ax+ ![]() a2=0,若双曲线C1 的一条渐近线与圆 C2 有两个不同的交点,则双曲线 C1 的离心率的范围是( )
a2=0,若双曲线C1 的一条渐近线与圆 C2 有两个不同的交点,则双曲线 C1 的离心率的范围是( )
A.(1, ![]() )
)
B.( ![]() ,+∞)
,+∞)
C.(1,2)
D.(2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,双曲线的中心在坐标原点O,M、N分别为双曲线虚轴的上、下端点,A是双曲线的右顶点,F是双曲线的右焦点,直线AM与FN相交于点P,若∠APF是锐角,则此双曲线的离心率的取值范围是( ) 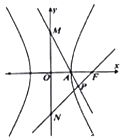
A.( ![]() ,+∞)
,+∞)
B.(1+ ![]() ,+∞)
,+∞)
C.(0, ![]() )
)
D.( ![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 上的动点P与其顶点
上的动点P与其顶点 ![]() ,
, ![]() 不重合. (Ⅰ)求证:直线PA与PB的斜率乘积为定值;
不重合. (Ⅰ)求证:直线PA与PB的斜率乘积为定值;
(Ⅱ)设点M,N在椭圆C上,O为坐标原点,当OM∥PA,ON∥PB时,求△OMN的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图:四棱锥P﹣ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=AB=1,AD= ![]() ,点F是PB的中点,点E在边BC上移动.
,点F是PB的中点,点E在边BC上移动. 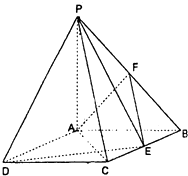
(1)证明:无论点E在BC边的何处,都有PE⊥AF;
(2)当BE等于何值时,PA与平面PDE所成角的大小为45°.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标xOy中,直线l的参数方程为{  (t为参数)在以O为极点.x轴正半轴为极轴的极坐标系中.曲线C的极坐标方程为ρ=4sinθ﹣2cosθ. (I)求直线l的普通方程与曲线C的直角坐标方程:
(t为参数)在以O为极点.x轴正半轴为极轴的极坐标系中.曲线C的极坐标方程为ρ=4sinθ﹣2cosθ. (I)求直线l的普通方程与曲线C的直角坐标方程:
(Ⅱ)若直线l与y轴的交点为P,直线l与曲线C的交点为A,B,求|PA||PB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等差数列{an}前n项和为Sn , 且S5=45,S6=60.
(1)求{an}的通项公式an;
(2)若数列{an}满足bn+1﹣bn=an(n∈N*)且b1=3,求{ ![]() }的前n项和Tn .
}的前n项和Tn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com