
【题目】已知数列{an}是等比数列,a1=2,a3=18.数列{bn}是等差数列,b1=2,b1+b2+b3+b4=a1+a2+a3>20.
(1)求数列{an},{bn}的通项公式;
(2)设Pn=b1+b4+b7+…+b3n﹣2 , Qn=b10+b12+b14+…+b2n+8 , 其中n=1,2,3,….试比较Pn与Qn的大小,并证明你的结论.
【答案】
(1)解:设{an}的公比为q,由a3=a1q2得q2= ![]() =9,q=±3.
=9,q=±3.
①当q=﹣3时,a1+a2+a3=2﹣6+18=14<20,
这与a1+a2+a3>20矛盾,故舍去.
②当q=3时,a1+a2+a3=2+6+18=26>20,故符合题意.
∴an=a1qn﹣1=2×3n﹣1
设数列{bn}的公差为d,由b1+b2+b3+b4=a1+a2+a3=26,
得4b1+ ![]() d=26,结合b1=2,解之得d=3,
d=26,结合b1=2,解之得d=3,
所以bn=bn+(n﹣1)d=2+3(n﹣1)=3n﹣1
综上所述,数列{an},{bn}的通项公式分别为an=2×3n﹣1、bn=3n﹣1;
(2)解:∵b1,b4,b7,…,b3n﹣2组成以3d为公差的等差数列,
∴Pn=nb1+ ![]() 3d=
3d= ![]() n2﹣
n2﹣ ![]() n;
n;
同理可得:b10,b12,b14,…,b2n+8组成以2d为公差的等差数列,且b10=29,
∴Qn=nb10+ ![]() 2d=3n2+26n.
2d=3n2+26n.
因此,Pn﹣Qn=( ![]() n2﹣
n2﹣ ![]() n)﹣(3n2+26n)=
n)﹣(3n2+26n)= ![]() n(n﹣19).
n(n﹣19).
所以对于正整数n,当n≥20时,Pn>Qn;当n=19时,Pn=Qn;当n≤18时,Pn<Qn.
【解析】(1)由等比数列通项公式,结合题意算出数列{an}的公比q=±3.讨论可得当q=﹣3时与题意矛盾,故q=3可得an=2×3n﹣1 . 由此得到{bn}的前4项和等于a1+a2+a3=26,利用等差数列的通项公式算出公差d=3,得bn=3n﹣1;(2)根据等差数列的性质,可得b1 , b4 , b7 , …,b3n﹣2和b10 , b12 , b14 , …,b2n+8分别组成以3d、2d为公差的等差数列,由等差数列求和公式算出Pn= ![]() n2﹣
n2﹣ ![]() n、Qn=3n2+26n.作差后,因式分解得Pn﹣Qn=
n、Qn=3n2+26n.作差后,因式分解得Pn﹣Qn= ![]() n(n﹣19),结合n为正整数加以讨论,即可得到Pn与Qn的大小关系,从而使本题得到解决.
n(n﹣19),结合n为正整数加以讨论,即可得到Pn与Qn的大小关系,从而使本题得到解决.
【考点精析】解答此题的关键在于理解数列的前n项和的相关知识,掌握数列{an}的前n项和sn与通项an的关系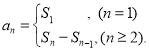 .
.


科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)的左右焦点分别为F1 , F2 , 点
=1(a>b>0)的左右焦点分别为F1 , F2 , 点 ![]() 为短轴的一个端点,∠OF2B=60°.
为短轴的一个端点,∠OF2B=60°.
(Ⅰ)求椭圆C的方程;
(Ⅱ)如图,过右焦点F2 , 且斜率为k(k≠0)的直线l与椭圆C相交于D,E两点,A为椭圆的右顶点,直线AE,AD分别交直线x=3于点M,N,线段MN的中点为P,记直线PF2的斜率为k′.试问kk′是否为定值?若为定值,求出该定值;若不为定值,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合M={x|﹣2<x<2},N={x|x2﹣2x﹣3<0},则集合M∩N=( )
A.{x|x<﹣2}
B.{x|x>3}
C.{x|﹣1<x<2}
D.{x|2<x<3}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+|x﹣a|+1,x∈R,a∈R.
(Ⅰ)当a=1时,求函数f(x)的最小值;
(Ⅱ)若函数f(x)的最小值为g(a),令m=g(a),求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】命题p:关于x的不等式x2+2ax+4>0对一切x∈R恒成立;命题q:函数f(x)=lagax在(0,+∞)上递增,若p∨q为真,而p∧q为假,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某农场预算用5600元购买单价为50元(每吨)的钾肥和20元(每吨)的氮肥,希望使两种肥料的总数量(吨)尽可能的多,但氮肥数不少于钾肥数,且不多于钾肥数的1.5倍.
(Ⅰ)设买钾肥x吨,买氮肥y吨,按题意列出约束条件、画出可行域,并求钾肥、氮肥各买多少才行?
(Ⅱ)已知A(10,0),O是坐标原点,P(x,y)在(Ⅰ)中的可行域内,求  的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com