
【题目】已知函数f(x)=x2﹣2x,g(x)=ax+2(a>0),若对任意x1∈R,都存在x2∈[﹣2,+∞),使得f(x1)>g(x2),则实数a的取值范围是( )
A.![]()
B.(0,+∞)
C.![]()
D.![]()
【答案】A
【解析】解:∵函数f(x)=x2﹣2x的图象是开口向上的抛物线,且关于直线x=1对称∴f(x)的最小值为f(1)=﹣1,无最大值,
可得f(x1)值域为[﹣1,+∞),
又∵g(x)=ax+2(a>0),x2∈[﹣2,+∞),
∴g(x)=ax+2(a>0)为单调增函数,g(x2)值域为[g(﹣2),+∞),
即g(x2)∈[2﹣2a,+∞),
∵对任意的x1∈R都存在x2∈[﹣2,+∞),使得f(x1)>g(x2),
∴只需f(x)值域是g(x)值域的子集即可,
∴2﹣2a<﹣1,解得:a> ![]() ,
,
故选:A.
【考点精析】根据题目的已知条件,利用全称命题的相关知识可以得到问题的答案,需要掌握全称命题![]() :
:![]() ,
,![]() ,它的否定
,它的否定![]() :
:![]() ,
,![]() ;全称命题的否定是特称命题.
;全称命题的否定是特称命题.


科目:高中数学 来源: 题型:
【题目】如图,已知A为左顶点,F是左焦点,l交OA的延长线于点B,点P,Q在椭圆上,有PD⊥l于点D,QF⊥AO,则椭圆的离心率是① ![]() ; ②
; ② ![]() ; ③
; ③ ![]() ; ④
; ④ ![]() ; ⑤
; ⑤ ![]() 其中正确的是( )
其中正确的是( )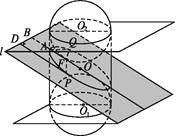
A.①②
B.①③④
C.②③⑤
D.①②③④⑤
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知不等式ax2+5x+b>0的解集是{x|2<x<3},则不等式bx2﹣5x+a>0的解集是( )
A.{x|x<﹣3或x>﹣2}
B.{x|x<﹣ ![]() 或x>﹣
或x>﹣ ![]() }
}
C.{x|﹣ ![]() <x<﹣
<x<﹣ ![]() }
}
D.{x|﹣3<x<﹣2}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=alnx﹣x2+1.
(Ⅰ)若曲线y=f(x)在x=1处的切线方程为4x﹣y+b=0,求实数a和b的值;
(Ⅱ)讨论函数f(x)的单调性;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】三棱锥P﹣ABC中,已知PA=PB=PC=AC=4,BC= ![]() AB=2
AB=2 ![]() ,O为AC中点.
,O为AC中点. 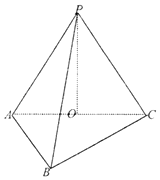
(1)求证:PO⊥平面ABC;
(2)求异面直线AB与PC所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆C的中心在坐标原点,焦点在x轴上,该椭圆经过点 ![]() 且离心率为
且离心率为 ![]() .
.
(1)求椭圆C的标准方程;
(2)若直线l:y=kx+m与椭圆C相交A,B两点(A,B不是左右顶点),且以AB为直径的圆过椭圆C的右顶点,求证:直线l过定点,并求出该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)是定义在[﹣1,1]上的奇函数,且对任意a、b∈[﹣1,1],当a+b≠0时,都有 ![]() >0.
>0.
(1)若a>b,比较f(a)与f(b)的大小;
(2)解不等式f(x﹣ ![]() )<f(x﹣
)<f(x﹣ ![]() );
);
(3)记P={x|y=f(x﹣c)},Q={x|y=f(x﹣c2)},且P∩Q=,求c的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com