
设函数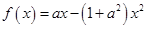 (
(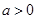 ).区间
).区间 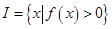 ,定义区间
,定义区间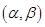 的长度为 b-a .
的长度为 b-a .
(1)求区间I的长度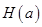 (用 a 表示);
(用 a 表示);
(2)若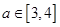 ,求
,求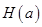 的最大值.
的最大值.
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源: 题型:解答题
假设若干杯甜度相同的糖水,分别经过下面的试验:
(1)①将所有糖水倒在一起;
②将任意多杯糖水倒在一起.
(2)将某一杯糖水中再加入一小匙糖,糖全都溶化.类经这些实验,分别能得到数学上怎样的关系式?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com