
【题目】已知函数![]() ,其中无理数
,其中无理数![]() .
.
(Ⅰ)若函数![]() 有两个极值点,求
有两个极值点,求![]() 的取值范围;
的取值范围;
(Ⅱ)若函数![]() 的极值点有三个,最小的记为
的极值点有三个,最小的记为![]() ,最大的记为
,最大的记为![]() ,若
,若![]() 的最大值为
的最大值为![]() ,求
,求![]() 的最小值.
的最小值.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】分析:(Ⅰ)先对函数![]() 求导,构造
求导,构造![]() ,则函数
,则函数![]() 有两个极值点等价于
有两个极值点等价于![]()
![]() 有两个不等的正实根,对函数
有两个不等的正实根,对函数![]() 求导,然后对
求导,然后对![]() 和
和![]() 进行讨论,可得函数
进行讨论,可得函数![]() 的单调性,结合
的单调性,结合![]() ,即可求得
,即可求得![]() 的取值范围;(Ⅱ)对函数
的取值范围;(Ⅱ)对函数![]() 求导,由
求导,由![]() 有三个极值点,则
有三个极值点,则![]() 有三个零点,1为一个零点,其他两个则为
有三个零点,1为一个零点,其他两个则为![]() 的零点,结合(Ⅰ),可得
的零点,结合(Ⅰ),可得![]() 的两个零点即为
的两个零点即为![]() 的最小和最大极值点
的最小和最大极值点![]() ,
,![]() ,即
,即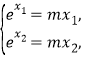 ,令
,令![]() ,由题知
,由题知![]() ,则
,则![]() ,令
,令![]() ,利用导数研究函数
,利用导数研究函数![]() 的单调性,从而可求得
的单调性,从而可求得![]() 的最小值即
的最小值即![]() 的最小值.
的最小值.
详解:(Ⅰ)![]() ,
,
令![]() ,
,![]() ,
,
∵![]() 有两个极值点
有两个极值点
∴![]()
![]() 有两个不等的正实根
有两个不等的正实根
∵![]()
∴当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增,不符合题意.
上单调递增,不符合题意.
当![]() 时,当
时,当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
∴![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
又∵![]() ,当
,当![]() →
→![]() 时,
时,![]() →
→![]()
∴![]()
∴![]()
综上,![]() 的取值范围是
的取值范围是![]() .
.
(Ⅱ)![]() .
.
∵![]() 有三个极值点
有三个极值点
∴![]() 有三个零点,1为一个零点,其他两个则为
有三个零点,1为一个零点,其他两个则为![]() 的零点,由(Ⅰ)知
的零点,由(Ⅰ)知![]() .
.
∵![]()
∴![]() 的两个零点即为
的两个零点即为![]() 的最小和最大极值点
的最小和最大极值点![]() ,
,![]() ,即
,即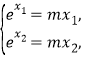 .
.
∴![]()
令![]() ,由题知
,由题知![]() .
.
∴![]() ,
,![]() ,
,![]()
∴![]()
令![]() ,
,![]() ,则
,则![]() ,令
,令![]() ,则
,则![]() .
.
∴![]() 在
在![]() 上单调递增
上单调递增
∴![]()
∴![]() 在
在![]() 上单调递减
上单调递减
∴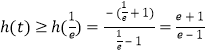
故![]() 的最小值为
的最小值为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某公司为了适应市场需求对产品结构做了重大调整,调整后初期利润增长迅速,之后增长越来越慢,若要建立恰当的函数模型来反映该公司调整后利润![]() 与时间
与时间![]() 的关系,可选用
的关系,可选用
A.一次函数B.二次函数
C.指数型函数D.对数型函数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在吸烟与患肺病是否相关的判断中,有下面的说法:
(1)从独立性分析可知在犯错误的概率不超过0.05的前提下,认为吸烟与患肺病有关系时,是指有![]() 的可能性使得推断错误.
的可能性使得推断错误.
(2)从独立性分析可知在犯错误的概率不超过0.01的前提下,认为吸烟与患肺病有关系时,若某人吸烟,则他有![]() 的可能患有肺病;
的可能患有肺病;
(3)若![]() ,则在犯错误的概率不超过0.01的前提下,认为吸烟与患肺病有关系,那么在100个吸烟的人中必有99人患有肺病;
,则在犯错误的概率不超过0.01的前提下,认为吸烟与患肺病有关系,那么在100个吸烟的人中必有99人患有肺病;
其中说法正确的是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() ,如果存在实数
,如果存在实数![]() 使得
使得![]() ,那么称
,那么称![]() 为
为![]() 的生成函数.
的生成函数.
(1)函数![]() ,是否为
,是否为![]() 的生成函数?说明理由;
的生成函数?说明理由;
(2)设![]() ,
,![]() ,当
,当![]() 时生成函数
时生成函数![]() ,求
,求![]() 的对称中心(不必证明);
的对称中心(不必证明);
(3)设![]() ,
,![]() ,取
,取![]() ,
,![]() ,生成函数
,生成函数![]() ,若函数
,若函数![]() 的最小值是5,求实数
的最小值是5,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=-2sin2x+sin 2x+1,给出下列四个命题:
①在区间![]() 上是减函数;
上是减函数;
②直线![]() 是函数图象的一条对称轴;
是函数图象的一条对称轴;
③函数f(x)的图象可由函数![]() 的图象向左平移
的图象向左平移![]() 而得到;
而得到;
④若![]() ,则f(x)的值域是
,则f(x)的值域是![]() .
.
其中正确命题序号是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() x2-aln x(a∈R).
x2-aln x(a∈R).
(1)若f(x)在x=2处取得极值,求a的值;
(2)求f(x)的单调区间;
(3)求证:当x>1时, ![]() x2+ln x<
x2+ln x<![]() x3.
x3.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数集![]() 具有性质
具有性质![]() ;对任意的
;对任意的![]() 、
、![]() ,
,![]() ,与
,与![]() 两数中至少有一个属于
两数中至少有一个属于![]() .
.
(1)分别判断数集![]() 与
与![]() 是否具有性质
是否具有性质![]() ,并说明理由;
,并说明理由;
(2)证明:![]() ,且
,且![]() ;
;
(3)当![]() 时,若
时,若![]() ,求集合
,求集合![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com