
【题目】设数列{an}的前n项和为Sn , a1=1,且nan+1=(n+2)Sn , n∈N* .
(1)求证:数列 ![]() 为等比数列;
为等比数列;
(2)求数列{Sn}的前n项和Tn .
【答案】
(1)证明:∵nan+1=(n+2)Sn,n∈N*.∴n(Sn+1﹣Sn)=(n+2)Sn,∴ ![]() =2×
=2× ![]() ,
,
∴数列 ![]() 为等比数列,首项为1,公比为2,
为等比数列,首项为1,公比为2,
(2)解:由(1)可得: ![]() =2n﹣1,∴Sn=n2n﹣1.
=2n﹣1,∴Sn=n2n﹣1.
∴数列{Sn}的前n项和Tn=1+2×2+3×2n+…+n2n﹣1.
∴2Tn=2+2×22+…+(n﹣1)2n﹣1+n2n,
∴﹣Tn=1+2+22+…+2n﹣1﹣n2n= ![]() ﹣n2n,
﹣n2n,
∴Tn=(n﹣1)2n+1.
【解析】(1)nan+1=(n+2)Sn , n∈N* . 可得n(Sn+1﹣Sn)=(n+2)Sn , 变形为 ![]() =2×
=2× ![]() ,即可证明.(2)由(1)可得:
,即可证明.(2)由(1)可得: ![]() =2n﹣1 , 可得Sn=n2n﹣1 . 利用“错位相减法”、等比数列的求和公式即可得出.
=2n﹣1 , 可得Sn=n2n﹣1 . 利用“错位相减法”、等比数列的求和公式即可得出.
【考点精析】认真审题,首先需要了解等比数列的通项公式(及其变式)(通项公式:![]() ),还要掌握数列的前n项和(数列{an}的前n项和sn与通项an的关系
),还要掌握数列的前n项和(数列{an}的前n项和sn与通项an的关系 )的相关知识才是答题的关键.
)的相关知识才是答题的关键.


 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sinxcos2x,下列结论正确的是( )
A.y=f(x)的图象关于 ![]() 对称
对称
B.y=f(x)的图象关于 ![]() 对称
对称
C.y=f(x)的图象关于y轴对称
D.y=f(x)不是周期函数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}是等差数列,Sn是其前n项和.已知a1+a3=16,S4=28.
(1)求数列{an}的通项公式
(2)当n取何值时Sn最大,并求出这个最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x(单位:m),修建此矩形场地围墙的总费用为y(单位:元). (Ⅰ)将y表示为x的函数:
(Ⅱ)试确定x,使修建此矩形场地围墙的总费用最小,并求出最小总费用.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,为了测量对岸A,B两点的距离,沿河岸选取C,D两点,测得CD=2km,∠CDB=∠ADB=30°,∠ACD=60°,∠ACB=45°,求A,B两点的距离. 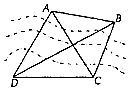
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an},{bn}满足a1=1,a2=2,b1=2,且对任意的正整数i,j,k,l,当i+j=k+l时,都有ai+bj=ak+bl , 则 ![]() 的值是( )
的值是( )
A.2012
B.2013
C.2014
D.2015
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两条直线 ![]() ,两个平面
,两个平面 ![]() ,给出下面四个命题:
,给出下面四个命题:
① ![]() ,
, ![]() ;②
;② ![]() ,
, ![]() ,
, ![]() ;
;
③ ![]() ,
, ![]() ;④
;④ ![]() ,
, ![]() ,
, ![]()
其中正确命题的序号是( )
A.①④
B.②④
C.①③
D.②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=2sin(2x+ ![]() )的图象为M,则下列结论中正确的是( )
)的图象为M,则下列结论中正确的是( )
A.图象M关于直线x=﹣ ![]() 对称
对称
B.由y=2sin2x的图象向左平移 ![]() 得到M
得到M
C.图象M关于点(﹣ ![]() ,0)对称
,0)对称
D.f(x)在区间(﹣ ![]() ,
, ![]() )上递增
)上递增
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com