练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    15．关于空间直角坐标系，下列叙述正确的是（　　）
    A．P（x，y，z）中x，y，z的位置可以互换的
    B．空间直角坐标系中的点与一个三元有序数组是一种一一对应关系
    C．空间直角坐标系中的三条坐标轴把空间分成八个部分
    D．某点在不同空间直角坐标系中的坐标位置可以相同

    分析 直接利用空间直角坐标系的性质判断即可．

    解答 解：A选项，x，y，z的位置不可以互换的，故A不正确；
    B选项，空间直角坐标系中的点与一个三元有序数组是一种一一对应关系，故B不正确；
    选项C，空间直角坐标系中的三条坐标轴把空间分成八个部分，故C正确．
    选项D，某点在不同空间直角坐标系中的坐标位置不可以相同，故D不正确；．
    故选：C．

    点评 本题考查空间直角坐标系的判断，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    5．在（1-2x）m的展开式中，第5项、第6项和第7项的二项式系数为等差数列，求展开式中的第2项．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．已知正项等差数列{an}满足a2+a4+a6=9，则log3（a1+$\frac{1}{2}{a}_{3}$+$\frac{1}{2}{a}_{5}$+a7）=2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．已知函数f（x）=log3（x+a），g（x）=log3（-x+2a-$\frac{1}{2}$），且f（4）-f（1）=1．
    （1）求a的值；
    （2）令F（x）=f（x）+g（x），判断函数F（x）的奇偶性．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．已知△ABC中，a=4，b=5，A=30°．下列对三角形解的情况的判断中，正确的是（　　）
    A．一解B．两解C．无解D．一解或无解

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．数列{an}满足an+1+an=2n-3，若a1=2，则a8-a4=4．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．编写一个程序，求使不等式1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{n}$＞10成立的最小自然数n的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    4．如图，在平行六面体ABCD-A1B1C1D1中，M为AC与D的交点，若$\overrightarrow{{A}_{1}{B}_{1}}$=$\overrightarrow{a}$，$\overrightarrow{A{{\;}_{1}D}_{1}}$=$\overrightarrow{b}$，$\overrightarrow{{A}_{1}A}$=$\overrightarrow{c}$，用基底{$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{c}$}表示向量$\overrightarrow{{C}_{1}M}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

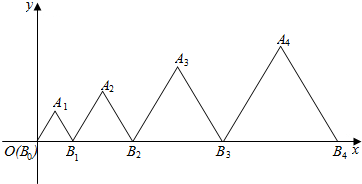    7．如图，在平面直角坐标系中，边长为an的一组正三角形AnBn-1Bn的底边Bn-1Bn依次排列在x轴上（B0与坐标原点重合）．设{an}是首项为a，公差为d的等差数列，若所有正三角形顶点An在第一象限，且均落在抛物线y2=2px（p＞0）上，则$\frac{a}{d}$的值为1．

    查看答案和解析>>

    同步练习册答案