
【题目】已知f(x)=(ex-a)2+(e-x-a)2(a≥0).
(1)将f(x)表示成u(其中u=![]() )的函数;
)的函数;
(2)求f(x)的最小值.
【答案】(1)g(u)=4u2-4au+2a2-2(u≥1)(2)f(x)min=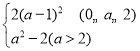
【解析】
(1)![]() 展开后整理成关于
展开后整理成关于![]() 的形式,换元即可(2)由(1)知换元后函数为关于
的形式,换元即可(2)由(1)知换元后函数为关于![]() 的二次函数,根据对称轴分类讨论即可求解.
的二次函数,根据对称轴分类讨论即可求解.
(1)将f(x)展开重新配方得,f(x)=(ex+e-x)2-2a(ex+e-x)+2a2-2.
令u=![]() ,则
,则![]() ,得g(u)=4u2-4au+2a2-2(u≥1).
,得g(u)=4u2-4au+2a2-2(u≥1).
(2)∵g(u)的对称轴是u=![]() ,a≥0,
,a≥0,
∴当0≤a≤2时,则当u=1时,g(u)有最小值,此时g(u)min=g(1)=2(a-1)2.
当a>2时,则当u=![]() 时,g(u)有最小值,此时g(u)min=g
时,g(u)有最小值,此时g(u)min=g![]() =a2-2.
=a2-2.
∴f(x)的最小值为f(x)min=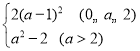


科目:高中数学 来源: 题型:
【题目】下列命题正确的有________(只填序号)
①若直线与平面有无数个公共点,则直线在平面内;
②若直线l上有无数个点不在平面α内,则l∥α;
③若两条异面直线中的一条与一个平面平行,则另一条直线一定与该平面相交;
④若直线l与平面α平行,则l与平面α内的直线平行或异面;
⑤若平面α∥平面β,直线aα,直线bβ,则直线a∥b.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设全集U=R,集合A={x|1≤x<4},B={x|2a≤x<3-a}.
(1)若a=-2,求B∩A,B∩(UA);(2)若A∪B=A,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC中, ![]() =λ
=λ ![]() (0<λ<1),cosC=
(0<λ<1),cosC= ![]() ,cos∠ADC=
,cos∠ADC= ![]() .
.
(1)若AC=5.BC=7,求AB的大小;
(2)若AC=7,BD=10,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点C为圆(x+1)2+y2=8的圆心,P是圆上的动点,点Q在圆的半径CP上,且有点A(1,0)和AP上的点M,满足 ![]()
![]() =0,
=0, ![]() =2
=2 ![]() .
.
(1)当点P在圆上运动时,求点Q的轨迹方程;
(2)若斜率为k的直线 l与圆x2+y2=1相切,直线 l与(1)中所求点Q的轨迹交于不同的两点F,H,O是坐标原点,且 ![]() ≤
≤ ![]()
![]() ≤
≤ ![]() 时,求k的取值范围.
时,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的定义域为{x|x∈R,且x≠0},对定义域内的任意x1、x2,都有f(x1·x2)=f(x1)+f(x2),且当x>1时,f(x)>0.
(1)求证:f(x)是偶函数;
(2)求证:f(x)在(0,+∞)上是增函数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com