
【题目】某科研机构为了研究喝酒与糖尿病是否有关,现对该市30名男性成人进行了问卷调查,并得到了如下列联表,规定“平均每天喝100ml以上的”为常喝.已知在所有的30人中随机抽取1人,是糖尿病的概率为![]() .
.
常喝 | 不常喝 | 合计 | |
有糖尿病 | 2 | ||
无糖尿病 | 18 | ||
合计 | 30 |
(1)请将上表补充完整;
(2)是否有![]() 的把握认为糖尿病与喝酒有关?请说明理由.
的把握认为糖尿病与喝酒有关?请说明理由.
(3)已知常喝酒且有糖尿病的人中恰有两名女性,现从常喝酒且有糖尿病的人中随机抽取2人,求恰好抽到一名男性和一名女性的概率.
参考公式:
参考数据:
|
|
|
|
|
|
| |
k |
|
|
|
|
|
|
|
【答案】(1)见详解;(2)有![]() 的把握认为糖尿病与喝酒有关;(3)
的把握认为糖尿病与喝酒有关;(3)![]()
【解析】
(1)由所有的30人中随机抽取1人,是糖尿病的概率为![]() ,可得出糖尿病人有8人,据此完善整个列联表;
,可得出糖尿病人有8人,据此完善整个列联表;
(2)计算观测值![]() ,对照数表得出结论;
,对照数表得出结论;
(3)用列举法,求出基本事件的个数,从而求出正好抽到一男一女的概率.
解:(1)![]() 所有的30人中随机抽取1人,是糖尿病的概率为
所有的30人中随机抽取1人,是糖尿病的概率为![]() ,
,
![]() 30人中,有糖尿病的有
30人中,有糖尿病的有![]() 人
人
常喝 | 不常喝 | 合计 | |
有糖尿病 | 6 | 2 | 8 |
无糖尿病 | 4 | 18 | 22 |
合计 | 10 | 20 | 30 |
(2)由列联表的数据可求得:
![]()
故有![]() 的把握认为糖尿病与喝酒有关;
的把握认为糖尿病与喝酒有关;
(3)设常喝酒且有糖尿病的男性为A、B、C、D,女性为a,b,
则任取两人有:AB,AC,AD,Aa,Ab,BC,BD,Ba,Bb,CD,
Ca,Cb,Da,Db,ab,共15种,
其中一男一女有:Aa,Ab,
故抽到一男一女的概率是![]() .
.


科目:高中数学 来源: 题型:
【题目】近期,某超市针对一款饮料推出刷脸支付活动,活动设置了一段时间的推广期,由于推广期内优惠力度较大,吸引越来越多的人开始使用刷脸支付.该超市统计了活动刚推出一周内每一天使用刷脸支付的人次,用![]() 表示活动推出的天数,
表示活动推出的天数,![]() 表示每天使用刷脸支付的人次,统计数据如下表所示:
表示每天使用刷脸支付的人次,统计数据如下表所示:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)在推广期内,![]() 与
与![]() (
(![]() 均为大于零的常数)哪一个适宜作为刷脸支付的人次
均为大于零的常数)哪一个适宜作为刷脸支付的人次![]() 关于活动推出天数
关于活动推出天数![]() 的回归方程类型?(给出判断即可,不必说明理由);
的回归方程类型?(给出判断即可,不必说明理由);
(2)根据(1)的判断结果及表![]() 中的数据,求
中的数据,求![]() 关于
关于![]() 的回归方程,并预测活动推出第
的回归方程,并预测活动推出第![]() 天使用刷脸支付的人次;
天使用刷脸支付的人次;
(3)已知一瓶该饮料的售价为![]() 元,顾客的支付方式有三种:现金支付、扫码支付和刷脸支付,其中有
元,顾客的支付方式有三种:现金支付、扫码支付和刷脸支付,其中有![]() 使用现金支付,使用现金支付的顾客无优惠;有
使用现金支付,使用现金支付的顾客无优惠;有![]() 使用扫码支付,使用扫码支付享受
使用扫码支付,使用扫码支付享受![]() 折优惠;有
折优惠;有![]() 使用刷脸支付,根据统计结果得知,使用刷脸支付的顾客,享受
使用刷脸支付,根据统计结果得知,使用刷脸支付的顾客,享受![]() 折优惠的概率为
折优惠的概率为![]() ,享受
,享受![]() 折优惠的概率为
折优惠的概率为![]() ,享受
,享受![]() 折优惠的概率为
折优惠的概率为![]() .根据所给数据估计购买一瓶该饮料的平均花费.
.根据所给数据估计购买一瓶该饮料的平均花费.
参考数据:其中![]() ,
,![]()
|
|
|
|
|
|
参考公式:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为:
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某家庭记录了未使用节水龙头50天的日用水量数据(单位:m3)和使用了节水龙头50天的日用水量数据,得到频数分布表如下:
未使用节水龙头50天的日用水量频数分布表
日用 水量 |
|
|
|
|
|
|
|
频数 | 1 | 3 | 2 | 4 | 9 | 26 | 5 |
使用了节水龙头50天的日用水量频数分布表
日用 水量 |
|
|
|
|
|
|
频数 | 1 | 5 | 13 | 10 | 16 | 5 |
(1)在答题卡上作出使用了节水龙头50天的日用水量数据的频率分布直方图:

(2)估计该家庭使用节水龙头后,日用水量小于0.35 m3的概率;
(3)估计该家庭使用节水龙头后,一年能节省多少水?(一年按365天计算,同一组中的数据以这组数据所在区间中点的值作代表.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某快递公司收取快递费用的标准是:重量不超过![]() 的包裹收费10元;重量超过
的包裹收费10元;重量超过![]() 的包裹,除收费10元之外,超过
的包裹,除收费10元之外,超过![]() 的部分,每超出
的部分,每超出![]() (不足
(不足![]() ,按
,按![]() 计算)需要再收费5元.该公司近60天每天揽件数量的频率分布直方图如下图所示(同一组数据用该区间的中点值作代表).
计算)需要再收费5元.该公司近60天每天揽件数量的频率分布直方图如下图所示(同一组数据用该区间的中点值作代表).
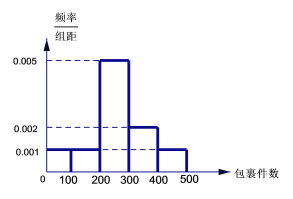
(1)求这60天每天包裹数量的平均值和中位数;
(2)该公司从收取的每件快递的费用中抽取5元作为前台工作人员的工资和公司利润,剩余的作为其他费用.已知公司前台有工作人员3人,每人每天工资100元,以样本估计总体,试估计该公司每天的利润有多少元?
(3)小明打算将![]() 四件礼物随机分成两个包裹寄出,且每个包裹重量都不超过
四件礼物随机分成两个包裹寄出,且每个包裹重量都不超过![]() ,求他支付的快递费为45元的概率.
,求他支付的快递费为45元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以原点
中,以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系. 已知曲线的极坐标方程为
轴的正半轴为极轴建立极坐标系. 已知曲线的极坐标方程为![]() ,直线 的参数方程为
,直线 的参数方程为 (
(![]() 为参数).
为参数).
(I)分别求曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(II)设曲线![]() 和直线
和直线![]() 相交于
相交于![]() 两点,求弦长
两点,求弦长![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定点F(1,0),定直线![]() ,动点M到点F的距离与到直线l的距离相等.
,动点M到点F的距离与到直线l的距离相等.
(1)求动点M的轨迹方程;
(2)设点![]() ,过点F作一条斜率大于0的直线交轨迹M于A,B两点,分别连接PA,PB,若直线PA与直线PB不关于x轴对称,求实数t的取值范围.
,过点F作一条斜率大于0的直线交轨迹M于A,B两点,分别连接PA,PB,若直线PA与直线PB不关于x轴对称,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一辆汽车前往目的地需要经过![]() 个有红绿灯的路口.汽车在每个路口遇到绿灯的概率为
个有红绿灯的路口.汽车在每个路口遇到绿灯的概率为![]() (可以正常通过),遇到红灯的概率为
(可以正常通过),遇到红灯的概率为![]() (必须停车).假设汽车只有遇到红灯或到达目的地才停止前进,用随机变量
(必须停车).假设汽车只有遇到红灯或到达目的地才停止前进,用随机变量![]() 表示前往目的地途中遇到红灯数和绿灯数之差的绝对值.
表示前往目的地途中遇到红灯数和绿灯数之差的绝对值.
(1)求汽车在第![]() 个路口首次停车的概率;
个路口首次停车的概率;
(2)求![]() 的概率分布和数学期望.
的概率分布和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com