
 ,且f(1)=2,
,且f(1)=2,
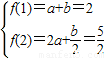 ,联立方程可求a,b
,联立方程可求a,b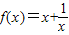 的定义域是否关于原点对称,然后检验f(-x)与f(x)的关系即可
的定义域是否关于原点对称,然后检验f(-x)与f(x)的关系即可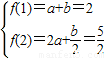 ,…(2分)
,…(2分) 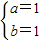 …(4分)
…(4分)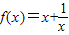 的定义域为(-∞,0)∪(0,+∞)关于原点对称,…(5分)
的定义域为(-∞,0)∪(0,+∞)关于原点对称,…(5分)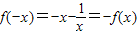
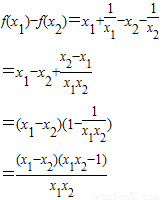


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:高中数学 来源:2012-2013学年安徽省黄山市屯溪一中高三(上)第三次月考数学试卷(文科)(解析版) 题型:解答题
 ,且f(1)=log162,f(-2)=1.
,且f(1)=log162,f(-2)=1.查看答案和解析>>
科目:高中数学 来源:2012-2013学年安徽省阜阳三中高一(上)第一次调研数学试卷(解析版) 题型:解答题
 ,且f(1)=2,
,且f(1)=2,
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江西省南昌外国语学校高三(上)11月月考数学试卷(理科)(解析版) 题型:解答题
 ,且f(1)=1,f(-2)=4.
,且f(1)=1,f(-2)=4. 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.查看答案和解析>>
科目:高中数学 来源:2011-2012学年广东省中山实验高中高一(上)10月段考试数学试卷(解析版) 题型:解答题
 ,且f(1)=3
,且f(1)=3查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com