
【题目】在平面直角坐标系![]() 中,对于直线
中,对于直线![]() 和点
和点![]() 、
、![]() ,记
,记![]() ,若
,若![]() ,则称点
,则称点![]() ,
,![]() 被直线l分隔,若曲线C与直线l没有公共点,且曲线C上存在点
被直线l分隔,若曲线C与直线l没有公共点,且曲线C上存在点![]() ,
,![]() 被直线l分隔,则称直线l为曲线C的一条分隔线.
被直线l分隔,则称直线l为曲线C的一条分隔线.
(1)求证:点![]() 、
、![]() 被直线
被直线![]() 分隔;
分隔;
(2)若直线![]() 是曲线
是曲线![]() 的分隔线,求实数
的分隔线,求实数![]() 的取值范围;
的取值范围;
(3)动点M到点![]() 的距离与到y轴的距离之积为1,设点M的轨迹为E,求E的方程,并证明y轴为曲线E的分隔线.
的距离与到y轴的距离之积为1,设点M的轨迹为E,求E的方程,并证明y轴为曲线E的分隔线.
【答案】(1)证明见解析(2)![]() (3)
(3)![]() ,证明见解析
,证明见解析
【解析】
(1)根据点![]() ,
,![]() 被直线l分隔的定义证明即可,
被直线l分隔的定义证明即可,
(2)先由直线与曲线无交点,利用判别式小于0可得![]() 的范围,然后在曲线上取两个点验证是否被直线分隔,
的范围,然后在曲线上取两个点验证是否被直线分隔,
(3)先求出轨迹![]() 的方程,然后证明轨迹方程与
的方程,然后证明轨迹方程与![]() 轴无交点,再在轨迹
轴无交点,再在轨迹![]() 上取两个点验证是否被
上取两个点验证是否被![]() 轴分隔.
轴分隔.
(1)由题意得:![]() ,
,
![]() 被直线
被直线![]() 分隔;
分隔;
(2)由题意得:直线![]() 与曲线
与曲线![]() 无交点,
无交点,
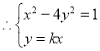 ,整理得
,整理得![]() 无解,即
无解,即![]()
![]() ,
,
又对任意的![]() ,点
,点![]() 和
和![]() 在曲线
在曲线![]() 上,满足
上,满足![]() ,所以点
,所以点![]() 和
和![]() 被直线
被直线![]() 分隔,
分隔,
![]() 所求的k的范围是
所求的k的范围是![]() .
.
(3)由题意得:设![]() ,
,![]() ,
,
化简得点M的轨迹方程为![]()
![]() 对任意的
对任意的![]() ,点
,点![]() 不是方程
不是方程![]() 的解
的解
![]() 直线
直线![]() 与曲线E没有交点,
与曲线E没有交点,
又曲线E上的两点![]() 和
和![]() 对于直线
对于直线![]() 满足
满足![]() ,
,
即点![]() 和
和![]() 被直线
被直线![]() 分隔,
分隔,
![]() 直线y轴是E的分隔线.
直线y轴是E的分隔线.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某学生将语文、数学、英语、物理、化学、生物6科的作业安排在周六、周日完成,要求每天至少完成两科,且数学,物理作业不在同一天完成,则完成作业的不同顺序种数为( )
A. 600B. 812C. 1200D. 1632
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() ,直线
,直线![]() ,设圆
,设圆![]() 的半径为1, 圆心在
的半径为1, 圆心在![]() 上.
上.

(1)若圆心![]() 也在直线
也在直线![]() 上,过点
上,过点![]() 作圆
作圆![]() 的切线,求切线方程;
的切线,求切线方程;
(2)若圆![]() 上存在点
上存在点![]() ,使
,使![]() ,求圆心
,求圆心![]() 的横坐标
的横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知拋物线![]() 的焦点为
的焦点为![]() 是抛物线上横坐标为4且位于
是抛物线上横坐标为4且位于![]() 轴上方的点,点
轴上方的点,点![]() 到抛物线准线的距离等于5.过点
到抛物线准线的距离等于5.过点![]() 作
作![]() 垂直于
垂直于![]() 轴,垂足为
轴,垂足为![]() 的中点为
的中点为![]() .
.
(1)求抛物线方程;
(2)过点![]() 作
作![]() ,垂足为
,垂足为![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)以点![]() 为圆心,
为圆心,![]() 为半径作圆
为半径作圆![]() ,当
,当![]() 是
是![]() 轴上一动点时,讨论直线
轴上一动点时,讨论直线![]() 与圆
与圆![]() 的位置关系.
的位置关系.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新高考方案的实施,学生对物理学科的选择成了焦点话题. 某学校为了了解该校学生的物理成绩,从![]() ,两个班分别随机调查了40名学生,根据学生的某次物理成绩,得到
,两个班分别随机调查了40名学生,根据学生的某次物理成绩,得到![]() 班学生物理成绩的频率分布直方图和
班学生物理成绩的频率分布直方图和![]() 班学生物理成绩的频数分布条形图.
班学生物理成绩的频数分布条形图.
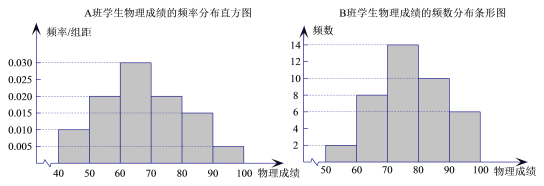
(Ⅰ)估计![]() 班学生物理成绩的众数、中位数(精确到
班学生物理成绩的众数、中位数(精确到![]() )、平均数(各组区间内的数据以该组区间的中点值为代表);
)、平均数(各组区间内的数据以该组区间的中点值为代表);
(Ⅱ)填写列联表,并判断是否有![]() 的把握认为物理成绩与班级有关?
的把握认为物理成绩与班级有关?
物理成绩 | 物理成绩 | 合计 | |
| |||
| |||
合计 |
附:![]() 列联表随机变量
列联表随机变量![]() ;
;
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“五一”期间,为了满足广大人民的消费需求,某共享单车公司欲投放一批共享单车,单车总数不超过100辆,现有A,B两种型号的单车:其中A型车为运动型,成本为400元![]() 辆,骑行半小时需花费
辆,骑行半小时需花费![]() 元;B型车为轻便型,成本为2400元
元;B型车为轻便型,成本为2400元![]() 辆,骑行半小时需花费1元
辆,骑行半小时需花费1元![]() 若公司投入成本资金不能超过8万元,且投入的车辆平均每车每天会被骑行2次,每次不超过半小时
若公司投入成本资金不能超过8万元,且投入的车辆平均每车每天会被骑行2次,每次不超过半小时![]() 不足半小时按半小时计算
不足半小时按半小时计算![]() ,问公司如何投放两种型号的单车才能使每天获得的总收入最多,最多为多少元?
,问公司如何投放两种型号的单车才能使每天获得的总收入最多,最多为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com