
【题目】如图,![]() ,
,![]() 是经过小城
是经过小城![]() 的东西方向与南北方向的两条公路,小城
的东西方向与南北方向的两条公路,小城![]() 位于小城
位于小城![]() 的东北方向,直线距离
的东北方向,直线距离![]() .现规划经过小城
.现规划经过小城![]() 修建公路
修建公路![]() (
(![]() ,
,![]() 分别在
分别在![]() 与
与![]() 上),与
上),与![]() ,
,![]() 围成三角形区域
围成三角形区域![]() .
.
(1)设![]() ,
,![]() ,求三角形区域
,求三角形区域![]() 周长的函数解析式
周长的函数解析式![]() ;
;
(2)现计划开发周长最短的三角形区域![]() ,求该开发区域的面积.
,求该开发区域的面积.

【答案】(1) ![]()
![]()
![]()
(2)开发区域![]() 的面积为
的面积为![]()
【解析】分析:(1)先根据直角三角形求OA,OB,AB,再相加得三角形区域![]() 周长的函数解析式
周长的函数解析式![]() ; (2) 令
; (2) 令![]() ,化简
,化简![]() ,再根据三角函数有界性确定t范围,解得
,再根据三角函数有界性确定t范围,解得![]() 最小值,同时求出开发区域的面积.
最小值,同时求出开发区域的面积.
详解:解:(方法一)
(1)如图,过![]() 分别作
分别作![]() 、
、![]() 的垂线,垂足分别为
的垂线,垂足分别为![]() 、
、![]() ,因为小城
,因为小城![]() 位于小城
位于小城![]() 的东北方向,且
的东北方向,且![]() ,所以
,所以![]() ,在
,在![]() 和
和![]() 中,易得
中,易得![]() ,
,![]()
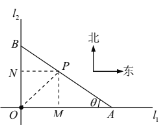
![]() ,
,![]()
所以![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
当![]() 时,
时,![]() ,
,![]() 单调递减
单调递减
当![]() 时,
时,![]() ,
,![]() 单调递增
单调递增
所以![]() 时,
时,![]() 取得最小值.
取得最小值.
此时,![]() ,
,![]()
![]() 的面积
的面积![]()
![]()
![]()
![]()
答:开发区域![]() 的面积为
的面积为![]()
(方法二)
(1)在![]() 中,
中,![]() ,即
,即![]()
所以![]()
在![]() 中,
中,![]()
![]()
![]()
![]()
所以![]()
![]()
![]()
![]()
![]()
![]()
(2)令![]() ,则
,则![]()
因为![]() ,所以
,所以![]() ,所以
,所以![]()
由![]()
![]() ,得
,得![]()
记![]()
![]()
![]()
![]()
因为![]() 在
在![]() 上单调递减,所以当
上单调递减,所以当![]() 时
时![]() 最小
最小
此时![]() ,即
,即![]()
![]()
 ,
,![]()
所以![]() 的面积
的面积![]()
![]()
![]()
![]()
答:开发区域![]() 的面积为
的面积为![]()


科目:高中数学 来源: 题型:
【题目】甲、乙两名同学参加一项射击比赛游戏,其中任何一人每射击一次击中目标得2分,未击中目标得0分.若甲、乙两人射击的命中率分别为 ![]() 和P,且甲、乙两人各射击一次得分之和为2的概率为
和P,且甲、乙两人各射击一次得分之和为2的概率为 ![]() .假设甲、乙两人射击互不影响,则P值为( )
.假设甲、乙两人射击互不影响,则P值为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的定义域为R,且f(2)=2,又函数f(x)的导函数y=f′(x)的图象如图所示,若两个正数a、b满足f(2a+b)<2,则 ![]() 的取值范围是( )
的取值范围是( ) 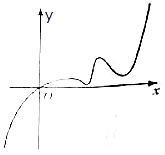
A.( ![]() ,2)
,2)
B.(﹣∞, ![]() )∪(2,+∞)
)∪(2,+∞)
C.(2,+∞)
D.(﹣∞, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)是定义在(﹣∞,0)上的可导函数,其导函数为f′(x),且有xf′(x)>x2+3f(x),则不等式8f(x+2014)+(x+2014)3f(﹣2)>0的解集为( )
A.(﹣∞,﹣2016)
B.(﹣2018,﹣2016)
C.(﹣2018,0)
D.(﹣∞,﹣2018)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图象如图所示(其中
的图象如图所示(其中![]() 是定义域为
是定义域为![]() 的函数
的函数![]() 的导函数),则以下说法错误的是( ).
的导函数),则以下说法错误的是( ).
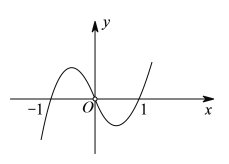
A. ![]()
B. 当![]() 时,函数
时,函数![]() 取得极大值
取得极大值
C. 方程![]() 与
与![]() 均有三个实数根
均有三个实数根
D. 当![]() 时,函数
时,函数![]() 取得极小值
取得极小值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】办公室装修一新,放些植物花草可以清除异味,公司提供绿萝、文竹、碧玉、芦荟4种植物供员工选择,每个员工任意选择2种,则员工甲和乙选择的植物全不同的概率为:
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com