
 与轨迹W交于A、B两点。
与轨迹W交于A、B两点。 ,求直线
,求直线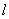 的方程;
的方程;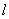 的任意一确定的位置,在直线x=
的任意一确定的位置,在直线x= 上是否存在一点Q,使得
上是否存在一点Q,使得 ,并说明理由。
,并说明理由。 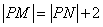 ,
,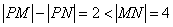 ,
, ,
,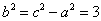 ,
,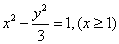 。
。 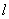 的斜率不存在时,显然不满足
的斜率不存在时,显然不满足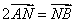 ,故
,故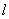 的斜率存在,
的斜率存在,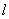 的方程为
的方程为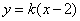 ,
,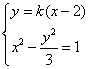 得
得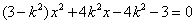 ,
,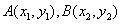 ,
,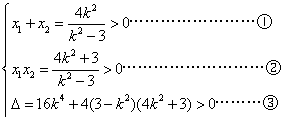 ,
,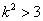 ,
,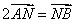 ,
,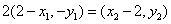 ,
,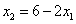 ,
,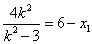 ,
,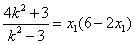 ,
,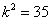 ,即
,即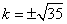 ,
,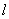 的方程为
的方程为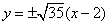 。
。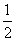 有公共点,若直线
有公共点,若直线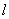 的斜率不存在,则以AB为直径的圆为
的斜率不存在,则以AB为直径的圆为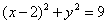 ,可知其与直线x=
,可知其与直线x=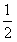 相交;
相交; 的斜率存在,则设直线
的斜率存在,则设直线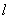 的方程为
的方程为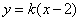 ,
,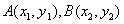 ,
,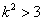 且
且 ,
,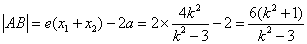 ,
,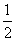 的距离为d,则
的距离为d,则 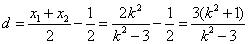 ,
,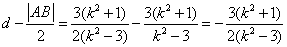 ,
,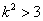 ,
,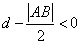 ,即
,即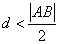 ,即直线
,即直线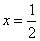 与圆S相交,
与圆S相交,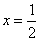 相交;
相交;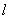 的任意一确定的位置,在直线
的任意一确定的位置,在直线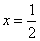 上存在一点Q(实际上存在两点)使得
上存在一点Q(实际上存在两点)使得 。
。 

 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:高中数学 来源: 题型:
| AN |
| NB |
| 1 |
| 2 |
| QA |
| QB |
查看答案和解析>>
科目:高中数学 来源:2010年湖北省襄阳市襄樊四中高考适应性考试数学试卷(文科)(解析版) 题型:解答题
 =
=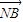 ,求直线l的方程;
,求直线l的方程; 上是否存在一点Q,使得
上是否存在一点Q,使得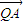 •
•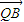 =0,并说明理由.
=0,并说明理由.查看答案和解析>>
科目:高中数学 来源:2011年河北省衡水市冀州中学高考数学一模试卷(理科)(解析版) 题型:解答题
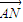 =
=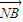 ,求直线l的方程;
,求直线l的方程; 上是否存在一点Q,使得
上是否存在一点Q,使得 •
•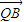 =0,并说明理由.
=0,并说明理由.查看答案和解析>>
科目:高中数学 来源:2011年高三数学单元检测:圆锥曲线(2)(解析版) 题型:解答题
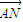 =
=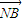 ,求直线l的方程;
,求直线l的方程; 上是否存在一点Q,使得
上是否存在一点Q,使得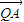 •
•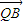 =0,并说明理由.
=0,并说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com