
【题目】已知抛物线C:x2=2py(p>0)的焦点为F.过F的直线与抛物线C交于A、B,与抛物线C的准线交于M.

(1)若|AF|=|FM|=4,求常数p的值;
(2)设抛物线C在点A、B处的切线相交于N,求动点N的轨迹方程.
【答案】(1)2;(2)y![]() .
.
【解析】
(1)设交点F(0,![]() ),则准线方程为y
),则准线方程为y![]() ,根据F为AM的中点可得
,根据F为AM的中点可得![]() y1
y1![]() 2p,即可求得
2p,即可求得![]() ;
;
(2)由![]() 可得
可得![]() ,即可求得切线斜率,联立抛物线与直线AB,根据韦达定理可得x1+x2=2pk,x1x2=﹣p2,利用点斜式直线方程可得在点
,即可求得切线斜率,联立抛物线与直线AB,根据韦达定理可得x1+x2=2pk,x1x2=﹣p2,利用点斜式直线方程可得在点![]() 的切线方程,联立即可求得点
的切线方程,联立即可求得点![]() ,即可得到点
,即可得到点![]() 的轨迹方程.
的轨迹方程.
(1)由抛物线的方程可得焦点坐标F(0,![]() ),准线方程为y
),准线方程为y![]() ,
,
设A(x1,y1),B(x2,y2),
因为|AF|=|FM|=4,所以F为AM的中点,所以y1![]() 2p,
2p,
所以2p=4,解得p=2
(2)由y![]() ,所以
,所以![]() ,设直线AB:y=kx
,设直线AB:y=kx![]() ,
,
与抛物线C的方程联立得:x2﹣2pkx﹣p2=0,则![]() =4p2k2+4p2>0,
=4p2k2+4p2>0,
所以x1+x2=2pk,x1x2=﹣p2,
则在点A处的切线方程为:y﹣y1![]() (x﹣x1),即py+py1=x1x,
(x﹣x1),即py+py1=x1x,
同理可得B处的切线方程py+py2=x2x,
联立 ,解得xN
,解得xN![]() pk,yN
pk,yN![]() ,
,
所以N的轨迹方程为y![]() ,
,


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:高中数学 来源: 题型:
【题目】里氏震级M的计算公式为:M=lgA﹣lgA0,其中A是测震仪记录的地震曲线的最大振幅,是相应的标准地震的振幅,假设在一次地震中,测震仪记录的最大振幅是1000,此时标准地震的振幅A0为0.001,则此次地震的震级为 级;9级地震的最大的振幅是5级地震最大振幅的 倍.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图象是由函数
的图象是由函数![]() 的图象经如下变换得到:先将函数
的图象经如下变换得到:先将函数![]() 图象上所有点的横坐标缩短到原来的
图象上所有点的横坐标缩短到原来的![]() 倍(纵坐标不变),再将所得到的图象向左平移
倍(纵坐标不变),再将所得到的图象向左平移![]() 个单位长度.
个单位长度.
(1)写出函数![]() 的解析式和其图象的对称中心坐标.
的解析式和其图象的对称中心坐标.
(2)已知关于![]() 的方程
的方程![]() 在
在![]() 上有两个不同的解
上有两个不同的解![]() ,
,![]() ,求实数
,求实数![]() 的取值范围和
的取值范围和![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C的对边分别为a,b,c,已知△ABC的面积为![]()
(1)求sinBsinC;
(2)若6cosBcosC=1,a=3,求△ABC的周长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=4x与椭圆E:![]() 1(a>b>0)有一个公共焦点F.设抛物线C与椭圆E在第一象限的交点为M.满足|MF|
1(a>b>0)有一个公共焦点F.设抛物线C与椭圆E在第一象限的交点为M.满足|MF|![]() .
.

(1)求椭圆E的标准方程;
(2)过点P(1,![]() )的直线交抛物线C于A、B两点,直线PO交椭圆E于另一点Q.若P为AB的中点,求△QAB的面积.
)的直线交抛物线C于A、B两点,直线PO交椭圆E于另一点Q.若P为AB的中点,求△QAB的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年,随着中国第一款5G手机投入市场,5G技术已经进入高速发展阶段.已知某5G手机生产厂家通过数据分析,得到如下规律:每生产手机![]() 万台,其总成本为
万台,其总成本为![]() ,其中固定成本为800万元,并且每生产1万台的生产成本为1000万元(总成本=固定成本+生产成本),销售收入
,其中固定成本为800万元,并且每生产1万台的生产成本为1000万元(总成本=固定成本+生产成本),销售收入![]() 万元满足
万元满足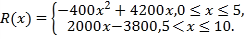
(1)将利润![]() 表示为产量
表示为产量![]() 万台的函数;
万台的函数;
(2)当产量![]() 为何值时,公司所获利润最大?最大利润为多少万元?
为何值时,公司所获利润最大?最大利润为多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com