
【题目】在直角坐标系![]() 中,点
中,点![]() ,圆
,圆![]() 的圆心为
的圆心为![]() ,半径为2.
,半径为2.
(Ⅰ)若![]() ,直线
,直线![]() 经过点
经过点![]() 交圆
交圆![]() 于
于![]() 、
、![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的方程;
的方程;
(Ⅱ)若圆![]() 上存在点
上存在点![]() 满足
满足![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】已知圆![]() 的方程为
的方程为![]() ,直线l的方程为
,直线l的方程为![]() ,点P在直线l上,过点P作圆
,点P在直线l上,过点P作圆![]() 的切线PA,PB,切点为A,B.
的切线PA,PB,切点为A,B.
(1)若![]() ,求点P的坐标;
,求点P的坐标;
(2)求证:经过A,P,![]() 三点的圆必经过异于
三点的圆必经过异于![]() 的某个定点,并求该定点的坐标.
的某个定点,并求该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合S={1,2,3,4,5,6},一一映射f:S→S满足条件:对于任意的x∈S,有f(f(f(x)))=x。则满足条件的映射f的个数是( )。
A. 81 B. 80 C. 40 D. 27
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现需要设计一个仓库,它由上下两部分组成,上部的形状是正四棱锥P—A1B1C1D1,下部的形状是正四棱柱ABCD—A1B1C1D1(如图所示),并要求正四棱柱的高O1O是正四棱锥的高PO1的4倍.
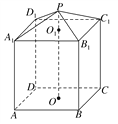
(1)若AB=6 m,PO1=2 m,则仓库的容积是多少?
(2)若正四棱锥的侧棱长为6 m,则当PO1为多少时,仓库的容积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确的个数是( )
①由五个面围成的多面体只能是三棱柱;
②由若干个平面多边形所围成的几何体是多面体;
③仅有一组对面平行的五面体是棱台;
④有一面是多边形,其余各面是三角形的几何体是棱锥.
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,圆台的上、下底面半径分别为5cm,10cm,母线长![]() ,从圆台母线
,从圆台母线![]() 的中点
的中点![]() 拉一条绳子绕圆台侧面转到
拉一条绳子绕圆台侧面转到![]() 点.求:
点.求:

(1)绳子的最短长度;
(2)在绳子最短时,求上底面圆周上的点到绳子的最短距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com