
已知圆C: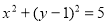 ,直线L:
,直线L: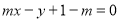 .
.
(1)求证:对 直线L与圆C总有两个不同交点;
直线L与圆C总有两个不同交点;
(2)设L与圆C交于不同两点A、B,求弦AB的中点M的轨迹方程;
(3)若定点P(1,1)分弦AB所得向量满足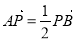 ,求此时直线L的方程.
,求此时直线L的方程.
(1)详见解析;(2)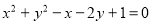 ;(3)直线方程为
;(3)直线方程为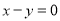 或
或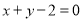 .
.
【解析】
试题分析:(1)由直线L的方程可知,直线L恒过定点(1,1),而这个点在圆内,所以直线L与圆C总有两个不同的交点;(2)设M(x,y).当M不与P重合时,连接CM、CP,由于P是AB的中点,所以CM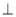 MP,用勾股定理便可得所求方程(或用向量的数量积等于0也可).(3)设A(
MP,用勾股定理便可得所求方程(或用向量的数量积等于0也可).(3)设A(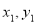 ),B(
),B(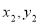 )由
)由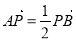 可得
可得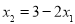 .将直线与圆的方程联立得
.将直线与圆的方程联立得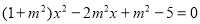 .由韦达定理得
.由韦达定理得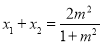 ,再将此与
,再将此与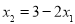 联立得
联立得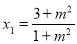 ,代入方程
,代入方程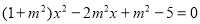 得
得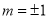 ,从而得直线的方程.
,从而得直线的方程.
试题解析:(1)直线恒过定点(1,1),且这个点在圆内,故直线L与圆C总有两个不同的交点.
(2)当M不与P重合时,连接CM、CP,则CM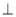 MP,设M(x,y)
MP,设M(x,y)
则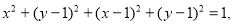
化简得: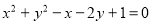
当M与P重合时,满足上式.
(3)设A(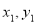 ),B(
),B(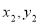 )由
)由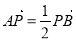 得
得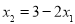 .
.
将直线与圆的方程联立得: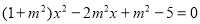 ..(*)
..(*)
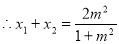
可得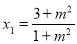 ,代入(*)得
,代入(*)得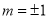
直线方程为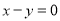 或
或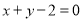 .
.
考点:直线与圆.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:高中数学 来源:2013-2014学年天津市南开区高三第一次模拟考试文科数学试卷(解析版) 题型:选择题
设定义域为R的函数 若关于x的方程
若关于x的方程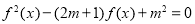 有7个不同的实数解,则m=( ).
有7个不同的实数解,则m=( ).
(A)2 (B)4或6 (C)2或6 (D)6
查看答案和解析>>
科目:高中数学 来源:2013-2014学年四川省高三下学期3月月考理科数学试卷(解析版) 题型:填空题
设z=kx+y,其中实数x、y满足 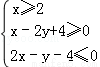 , 若z的最大值为12,则实数k= .
, 若z的最大值为12,则实数k= .
查看答案和解析>>
科目:高中数学 来源:2013-2014学年四川省高三下学期3月月考理科数学试卷(解析版) 题型:选择题
已知某几何体的三视图如图所示,则该几何体的体积为( )

A.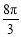 B.
B.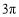 C.
C.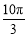 D.
D.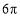
查看答案和解析>>
科目:高中数学 来源:2013-2014学年四川省高三下学期3月月考文科数学试卷(解析版) 题型:填空题
数列{an}满足an+1+(-1)n an =2n-1,则{an}的前60项和为____________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年四川省高三下学期3月月考文科数学试卷(解析版) 题型:选择题
若变量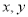 满足约束条件
满足约束条件 且
且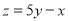 的最大值为
的最大值为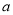 ,最小值为
,最小值为 ,则
,则 的值是( )
的值是( )
(A)16 (B)24 (C)30 (D)48
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com